Giả sử $z$ là số phức thỏa mãn $|i z-2-i|=3$. Giá trị lớn nhất của...

Ta có: $|i z-2-i|=3 \Leftrightarrow|i| .\left|z-\dfrac{2+i}{i}\right|=3 \Leftrightarrow|z-1+2 i|=3(1)$
Gọi $z=a+b i$ với $a, b \in \mathbb{R}$.
Từ (1), ta có $(a-1)^2+(b+2)^2=9 \Rightarrow\left\{\begin{array}{l}a=1+3 \sin t \\ b=-2+3 \cos t\end{array}(t \in \mathbb{R})\right.$.
Suy ra $z=(1+3 \sin t)+(-2+3 \operatorname{cost}) i$.
Đặt $P=2|z-4-i|+|z+5+8 i|$. Khi đó:
$
\begin{aligned}
P & =2 \sqrt{(-3+3 \sin t)^2+(-3+3 \cos t)^2}+\sqrt{(6+3 \sin t)^2+(6+3 \cos t)^2} \\
& =6 \sqrt{3-2 \sin t-2 \cos t}+3 \sqrt{9+4 \sin t+4 \cos t}=6 \sqrt{3-2 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)}+3 \sqrt{9+4 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)}
\end{aligned}
$
Đặt $u=\sin \left(t+\dfrac{\pi}{4}\right), u \in[-1 ; 1]$.
Xét hàm số $f(u)=6 \sqrt{3-2 \sqrt{2} u}+3 \sqrt{9+4 \sqrt{2} u}$ trên đoạn $[-1 ; 1]$
$
f^{\prime}(u)=\dfrac{-6 \sqrt{2}}{\sqrt{3-2 \sqrt{2} u}}+\dfrac{6 \sqrt{2}}{\sqrt{9+4 \sqrt{2} u}} \text {. Cho } f^{\prime}(u)=0 \Rightarrow u=\dfrac{-1}{\sqrt{2}} \in[-1 ; 1]
$
Ta có bảng biến thiên của hàm số $f(u)$ :
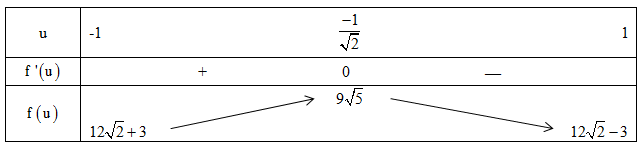Do vậy giá trj lớn nhất của $P$ là $9 \sqrt{5}$. Dấu bằng xảy ra khi $u=\dfrac{-1}{\sqrt{2}} \Rightarrow \sin \left(t+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}} \Leftrightarrow$
$
\left[\begin{array} { l }
{ t = - \dfrac { \pi } { 2 } + k 2 \pi } \\
{ t = - \pi + k 2 \pi }
\end{array} ( k \in \mathbb { Z } ) \Rightarrow \left[\begin{array}{l}
z=-2-2 i \\
z=1-5 i
\end{array}\right.\right.
$
Cách khác: Sử dụng Bất đẳng thức Bunhia đánh giá
$
\begin{aligned}
& P=6 \sqrt{3-2 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)}+3 \sqrt{9+4 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)} \\
& =3 \sqrt{2} \sqrt{6-4 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)}+3 \sqrt{9+4 \sqrt{2} \sin \left(t+\dfrac{\pi}{4}\right)} \leq \sqrt{(18+9)(6+9)}=9 \sqrt{5} .
\end{aligned}
$
Cách 2 (thông dụng hơn):
Ta có: $|i z-2-i|=3 \Leftrightarrow|i| .\left|z-\dfrac{2+i}{i}\right|=3 \Leftrightarrow|z-1+2 i|=3(1)$
Gọi $z=a+b i$ với $a, b \in \mathbb{R}$.
Từ (1), ta có $(a-1)^2+(b+2)^2=9 \Leftrightarrow a^2+b^2=2 a-4 b+4$.
Khi đó: $P=2 \sqrt{(a-4)^2+(b-1)^2}+\sqrt{(a+5)^2+(b+8)^2}$
$
\begin{aligned}
& =2 \sqrt{a^2+b^2-8 a-2 b+17}+\sqrt{a^2+b^2+10 a+16 b+89}=2 \sqrt{-6 a-6 b+21}+ \\
& \text { 考. } \sqrt{6 a+6 b+\dfrac{91}{2}} \\
& \leq \sqrt{(4+2)\left(21+\dfrac{93}{2}\right)}=\sqrt{405}=9 \sqrt{5}
\end{aligned}
$