Google
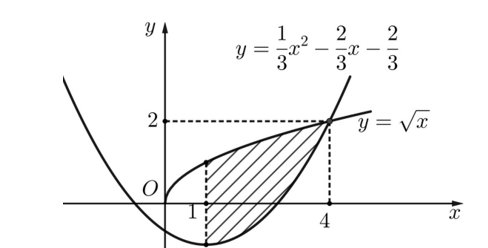
Câu hỏi: Diện tích phân gạch chéo trong hình vẽ được giới hạn bởi đồ thị của hai hàm số $y=\dfrac{1}{3}{{x}^{2}}-\dfrac{2}{3}x-\dfrac{2}{3}, y=\sqrt{x}$ và đường thẳng $x=1$ được tính bởi công thức
A. $S=\int\limits_{1}^{4}{\left( \dfrac{1}{3}{{x}^{2}}-\dfrac{2}{3}x-\dfrac{2}{3}-\sqrt{x} \right)\text{d}x}$.
B. $S=\dfrac{1}{3}\int\limits_{1}^{4}{\left( 3\sqrt{x}-{{x}^{2}}+2x+3 \right)\text{d}x}$.
C. $S=\int\limits_{0}^{4}{\left( \sqrt{x}-\dfrac{1}{3}{{x}^{2}}+\dfrac{2}{3}x+\dfrac{2}{3} \right)\text{d}x}$.
D. $S=\int\limits_{0}^{4}{\left( \dfrac{1}{3}{{x}^{2}}-\dfrac{2}{3}x-\dfrac{2}{3}-\sqrt{x} \right)\text{d}x}$.
B. $S=\dfrac{1}{3}\int\limits_{1}^{4}{\left( 3\sqrt{x}-{{x}^{2}}+2x+3 \right)\text{d}x}$.
C. $S=\int\limits_{0}^{4}{\left( \sqrt{x}-\dfrac{1}{3}{{x}^{2}}+\dfrac{2}{3}x+\dfrac{2}{3} \right)\text{d}x}$.
D. $S=\int\limits_{0}^{4}{\left( \dfrac{1}{3}{{x}^{2}}-\dfrac{2}{3}x-\dfrac{2}{3}-\sqrt{x} \right)\text{d}x}$.
Ta có $S=\int\limits_{1}^{4}{\left( \sqrt{x}-\dfrac{1}{3}{{x}^{2}}+\dfrac{2}{3}x+\dfrac{2}{3} \right)\text{d}x=}\dfrac{1}{3}\int\limits_{1}^{4}{\left( 3\sqrt{x}-{{x}^{2}}+2x+3 \right)\text{d}x}$.
Đáp án B.