Câu hỏi: Diện tích hình phẳng giới hạn bởi các đường: $y=\left| {{x}^{2}}-1 \right|$ và $y=\left| x \right|+5$ là:
A. $\dfrac{73}{6}$
B. $\dfrac{73}{3}$
C. 12
D. 14
A. $\dfrac{73}{6}$
B. $\dfrac{73}{3}$
C. 12
D. 14
Ta có: $y=\left| {{x}^{2}}-1 \right|=\left\{ \begin{aligned}
& {{x}^{2}}-1,x\le -1\vee x\ge 1 \\
& -\left( {{x}^{2}}-1 \right),-1<x<1 \\
\end{aligned} \right. $ và $ y=\left| x \right|+5=\left\{ \begin{aligned}
& x+5,x\ge 0 \\
& -x+5,x<0 \\
\end{aligned} \right.$
Ta có đồ thị
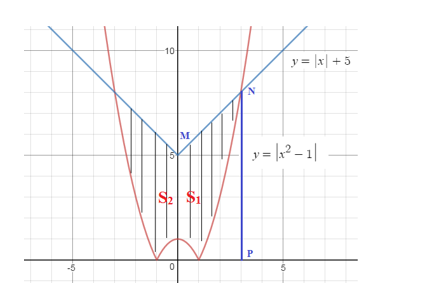
Hoành độ giao điểm dương của hai đường đã cho là nghiệm của phương trình:
${{x}^{2}}-1=x+5\Leftrightarrow {{x}^{2}}-x-6=0$, cho ta $x=3$.
Do tính chất đối xứng, diện tích S cần tìm bằng hai lần diện tích của S1, mà S1 = diện tích hình thang OMNP – I – J, với
$I=\int\limits_{0}^{1}{\left( -{{x}^{2}}+1 \right)d\text{x}}=\left[ -\dfrac{{{x}^{3}}}{3}+x \right]_{0}^{1}=\dfrac{2}{3}$ và $J=\int\limits_{1}^{3}{\left( {{x}^{2}}-1 \right)d\text{x}}=\left[ \dfrac{{{x}^{3}}}{3}-x \right]_{1}^{3}=\dfrac{20}{3}$ còn diện tích hình thang OMNP là $\dfrac{8+5}{2}\times 3=\dfrac{39}{2}$. Do vậy: ${{S}_{1}}=\dfrac{39}{2}-\dfrac{22}{3}=\dfrac{73}{6}$ (đvdt)
Từ đó, $S=\dfrac{73}{6}$
& {{x}^{2}}-1,x\le -1\vee x\ge 1 \\
& -\left( {{x}^{2}}-1 \right),-1<x<1 \\
\end{aligned} \right. $ và $ y=\left| x \right|+5=\left\{ \begin{aligned}
& x+5,x\ge 0 \\
& -x+5,x<0 \\
\end{aligned} \right.$
Ta có đồ thị
Hoành độ giao điểm dương của hai đường đã cho là nghiệm của phương trình:
${{x}^{2}}-1=x+5\Leftrightarrow {{x}^{2}}-x-6=0$, cho ta $x=3$.
Do tính chất đối xứng, diện tích S cần tìm bằng hai lần diện tích của S1, mà S1 = diện tích hình thang OMNP – I – J, với
$I=\int\limits_{0}^{1}{\left( -{{x}^{2}}+1 \right)d\text{x}}=\left[ -\dfrac{{{x}^{3}}}{3}+x \right]_{0}^{1}=\dfrac{2}{3}$ và $J=\int\limits_{1}^{3}{\left( {{x}^{2}}-1 \right)d\text{x}}=\left[ \dfrac{{{x}^{3}}}{3}-x \right]_{1}^{3}=\dfrac{20}{3}$ còn diện tích hình thang OMNP là $\dfrac{8+5}{2}\times 3=\dfrac{39}{2}$. Do vậy: ${{S}_{1}}=\dfrac{39}{2}-\dfrac{22}{3}=\dfrac{73}{6}$ (đvdt)
Từ đó, $S=\dfrac{73}{6}$
Đáp án A.