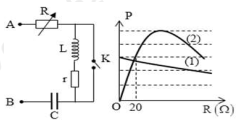
Câu hỏi: Đặt điện áp xoay chiều $u=U\sqrt{2}\cos \omega \text{t}$ (với U và ω không đổi) vào hai đầu đoạn mạch AB như hình vẽ. Biết R là biến trở, cuộn cảm thuần có độ tự cảm L, tụ điện có điện dung C thỏa mãn $LC{{\omega }^{2}}=2.$ Đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ P của mạch vào R trong trường hợp K mở ứng với đường (1) và trong trường hợp K đóng ứng với đường (2) như hình vẽ. Giá trị của điện trở r bằng
A. 90Ω
B. 60Ω
C. 180Ω
D. 20Ω

A. 90Ω
B. 60Ω
C. 180Ω
D. 20Ω
Phương pháp:
+ Đọc đồ thị
+ Khi K đóng mạch gồm RC mắc nối tiếp.
+ Khi K mở mạch gồm RLrC mắc nối tiếp.
+ Vận dụng biểu thức tính công suất: $P=UI\cos \varphi =\dfrac{{{U}^{2}}}{{{Z}^{2}}}R$
Cách giải:
Đặt 1ô theo phương OP có giá trị là a.
Theo đề bài, ta có: $LC{{\omega }^{2}}=2\Leftrightarrow \omega L=\dfrac{2}{\omega C}\Leftrightarrow {{Z}_{L}}=2{{\text{Z}}_{C}}$
+ Khi K đóng: ${{P}_{d}}=\dfrac{{{U}^{2}}}{{{R}^{2}}+Z_{C}^{2}}R$
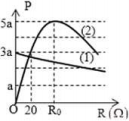
Từ đồ thị, ta thấy ${{P}_{{{d}_{\text{max }}}}}=5\text{a}=\dfrac{{{U}^{2}}}{2{{\text{R}}_{0}}}=\dfrac{{{U}^{2}}}{2{{\text{Z}}_{C}}}\text{ (1) }$
Và ${{P}_{{{d}_{\max }}}}\text{ khi }{{R}_{0}}={{Z}_{C}}>20\Omega $
Tại $R=20\Omega $, ta có: ${{P}_{d}}=\dfrac{{{U}^{2}}}{{{R}^{2}}+Z_{C}^{2}}R=\dfrac{{{U}^{2}}}{{{20}^{2}}+Z_{C}^{2}}\cdot 20=3\text{a}\left( 2 \right)$
Lấy $\dfrac{\left( 1 \right)}{\left( 2 \right)}$ ta được: $\dfrac{5}{3}=\dfrac{\dfrac{1}{2{{Z}_{C}}}}{\dfrac{20}{{{20}^{2}}+Z_{C}^{2}}}\Rightarrow \left[ \begin{array}{*{35}{l}}
{{Z}_{C}}=60\Omega \\
{{Z}_{C}}=\dfrac{20}{3}\Omega (\text{ loai }) \\
\end{array} \right.$
+ Khi K mở: ${{P}_{m}}=\dfrac{{{U}^{2}}}{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}(R+r)=\dfrac{{{U}^{2}}}{{{(R+r)}^{2}}+Z_{C}^{2}}(R+r)$
Từ đồ thị, ta thấy khi R = 0 thì ${{P}_{m}}=3\text{a}=\dfrac{{{U}^{2}}}{{{r}^{2}}+Z_{C}^{2}}\cdot r(3)$
Lấy $\dfrac{\left( 2 \right)}{\left( 3 \right)}$ ta được: $\dfrac{3}{3}=\dfrac{\dfrac{{{U}^{2}}}{{{20}^{2}}+Z_{C}^{2}}\cdot 20}{\dfrac{{{U}^{2}}}{{{r}^{2}}+Z_{C}^{2}}r}\Leftrightarrow 1=\dfrac{\dfrac{20}{{{20}^{2}}+{{60}^{2}}}}{\dfrac{r}{{{r}^{2}}+{{60}^{2}}}}\Rightarrow \left[ \begin{array}{*{35}{l}}
r=180\Omega \\
r=20\Omega \\
\end{array} \right.$
Do $r>\left| {{Z}_{L}}-{{Z}_{C}} \right|=60\Omega \Rightarrow r=180\Omega $
+ Đọc đồ thị
+ Khi K đóng mạch gồm RC mắc nối tiếp.
+ Khi K mở mạch gồm RLrC mắc nối tiếp.
+ Vận dụng biểu thức tính công suất: $P=UI\cos \varphi =\dfrac{{{U}^{2}}}{{{Z}^{2}}}R$
Cách giải:
Đặt 1ô theo phương OP có giá trị là a.
Theo đề bài, ta có: $LC{{\omega }^{2}}=2\Leftrightarrow \omega L=\dfrac{2}{\omega C}\Leftrightarrow {{Z}_{L}}=2{{\text{Z}}_{C}}$
+ Khi K đóng: ${{P}_{d}}=\dfrac{{{U}^{2}}}{{{R}^{2}}+Z_{C}^{2}}R$
Từ đồ thị, ta thấy ${{P}_{{{d}_{\text{max }}}}}=5\text{a}=\dfrac{{{U}^{2}}}{2{{\text{R}}_{0}}}=\dfrac{{{U}^{2}}}{2{{\text{Z}}_{C}}}\text{ (1) }$
Và ${{P}_{{{d}_{\max }}}}\text{ khi }{{R}_{0}}={{Z}_{C}}>20\Omega $
Tại $R=20\Omega $, ta có: ${{P}_{d}}=\dfrac{{{U}^{2}}}{{{R}^{2}}+Z_{C}^{2}}R=\dfrac{{{U}^{2}}}{{{20}^{2}}+Z_{C}^{2}}\cdot 20=3\text{a}\left( 2 \right)$
Lấy $\dfrac{\left( 1 \right)}{\left( 2 \right)}$ ta được: $\dfrac{5}{3}=\dfrac{\dfrac{1}{2{{Z}_{C}}}}{\dfrac{20}{{{20}^{2}}+Z_{C}^{2}}}\Rightarrow \left[ \begin{array}{*{35}{l}}
{{Z}_{C}}=60\Omega \\
{{Z}_{C}}=\dfrac{20}{3}\Omega (\text{ loai }) \\
\end{array} \right.$
+ Khi K mở: ${{P}_{m}}=\dfrac{{{U}^{2}}}{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}(R+r)=\dfrac{{{U}^{2}}}{{{(R+r)}^{2}}+Z_{C}^{2}}(R+r)$
Từ đồ thị, ta thấy khi R = 0 thì ${{P}_{m}}=3\text{a}=\dfrac{{{U}^{2}}}{{{r}^{2}}+Z_{C}^{2}}\cdot r(3)$
Lấy $\dfrac{\left( 2 \right)}{\left( 3 \right)}$ ta được: $\dfrac{3}{3}=\dfrac{\dfrac{{{U}^{2}}}{{{20}^{2}}+Z_{C}^{2}}\cdot 20}{\dfrac{{{U}^{2}}}{{{r}^{2}}+Z_{C}^{2}}r}\Leftrightarrow 1=\dfrac{\dfrac{20}{{{20}^{2}}+{{60}^{2}}}}{\dfrac{r}{{{r}^{2}}+{{60}^{2}}}}\Rightarrow \left[ \begin{array}{*{35}{l}}
r=180\Omega \\
r=20\Omega \\
\end{array} \right.$
Do $r>\left| {{Z}_{L}}-{{Z}_{C}} \right|=60\Omega \Rightarrow r=180\Omega $
Đáp án C.