Google
Câu hỏi: Có bao nhiêu số nguyên $a\in \left( -10 ; 10 \right)$ sao cho ứng với mỗi $a$ tồn tại ít nhất 5 số nguyên $b$ thỏa mãn ${{2}^{\dfrac{{{a}^{2}}+{{b}^{2}}}{ab}}}+\dfrac{a}{b}+1<\dfrac{a}{b}{{.2}^{\dfrac{b}{a}}}+\left( \dfrac{b}{a}+1 \right){{.2}^{\dfrac{a}{b}}}$ ?
A. $8$.
B. $6$.
C. $10$.
D. $12$.
A. $8$.
B. $6$.
C. $10$.
D. $12$.
Điều kiện xác định: $a,b\ne 0$. Đặt $u=\dfrac{a}{b},v=\dfrac{b}{a}\Rightarrow u.v=1$.
Từ giả thiết $\Rightarrow {{2}^{u+v}}+u+uv<u{{.2}^{v}}+\left( v+1 \right){{.2}^{u}}\Leftrightarrow {{2}^{u}}.\left( {{2}^{v}}-v-1 \right)-u\left( {{2}^{v}}-v-1 \right)<0$
$\Leftrightarrow \left( {{2}^{u}}-u \right)\left( {{2}^{v}}-1-v \right)<0$ (*)
Ta chứng minh ${{2}^{u}}-u>0, \forall u$. Thật vậy, xét hàm số $f(u)={{2}^{u}}-u\Rightarrow {f}'(u)={{2}^{u}}.\ln 2-1.$
Đạo hàm: ${f}'(u)=0\Leftrightarrow {{2}^{u}}=\dfrac{1}{\ln 2}\Leftrightarrow u={{\log }_{2}}\left( \dfrac{1}{\ln 2} \right)$.
Bảng biến thiên $f(u)$ :
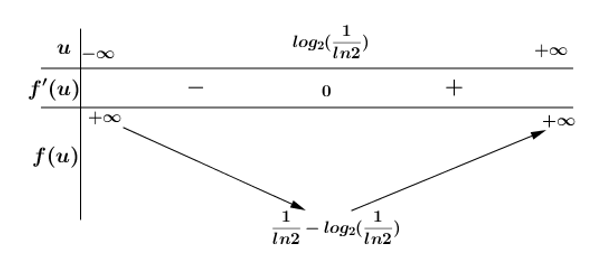Vì $\dfrac{1}{\ln 2}-{{\log }_{2}}\left( \dfrac{1}{\ln 2} \right)>0$ $\Rightarrow f(u)>0, \forall u$. Do đó (*) $\Leftrightarrow {{2}^{v}}-1-v<0\Leftrightarrow {{2}^{v}}-v<1$.
Từ bảng biến thiên ở trên, ta thấy $f(v)=1$ có nhiều nhất là 2 nghiệm. Dễ thấy $v=0,v=1$ là hai nghiệm thỏa mãn ${{2}^{v}}-v=1$ $\Rightarrow {{2}^{v}}-v<1\Leftrightarrow 0<v<1\Rightarrow 0<\dfrac{b}{a}<1$.
Nếu $a>0$ thì $0<\dfrac{b}{a}<1\Leftrightarrow 0<b<a$. Tồn tại ít nhất 5 số nguyên $b$ khi $a>5$.
Nếu $a<0$ thì $0<\dfrac{b}{a}<1\Leftrightarrow a<b<0$. Tồn tại ít nhất 5 số nguyên $b$ khi $a<-5$.
Kết hợp điều kiện $a\in \left( -10;10 \right)\Rightarrow a\in \left\{ 6;7;8;9;-6;-7;-8;-9 \right\}$.
Từ giả thiết $\Rightarrow {{2}^{u+v}}+u+uv<u{{.2}^{v}}+\left( v+1 \right){{.2}^{u}}\Leftrightarrow {{2}^{u}}.\left( {{2}^{v}}-v-1 \right)-u\left( {{2}^{v}}-v-1 \right)<0$
$\Leftrightarrow \left( {{2}^{u}}-u \right)\left( {{2}^{v}}-1-v \right)<0$ (*)
Ta chứng minh ${{2}^{u}}-u>0, \forall u$. Thật vậy, xét hàm số $f(u)={{2}^{u}}-u\Rightarrow {f}'(u)={{2}^{u}}.\ln 2-1.$
Đạo hàm: ${f}'(u)=0\Leftrightarrow {{2}^{u}}=\dfrac{1}{\ln 2}\Leftrightarrow u={{\log }_{2}}\left( \dfrac{1}{\ln 2} \right)$.
Bảng biến thiên $f(u)$ :
Từ bảng biến thiên ở trên, ta thấy $f(v)=1$ có nhiều nhất là 2 nghiệm. Dễ thấy $v=0,v=1$ là hai nghiệm thỏa mãn ${{2}^{v}}-v=1$ $\Rightarrow {{2}^{v}}-v<1\Leftrightarrow 0<v<1\Rightarrow 0<\dfrac{b}{a}<1$.
Nếu $a>0$ thì $0<\dfrac{b}{a}<1\Leftrightarrow 0<b<a$. Tồn tại ít nhất 5 số nguyên $b$ khi $a>5$.
Nếu $a<0$ thì $0<\dfrac{b}{a}<1\Leftrightarrow a<b<0$. Tồn tại ít nhất 5 số nguyên $b$ khi $a<-5$.
Kết hợp điều kiện $a\in \left( -10;10 \right)\Rightarrow a\in \left\{ 6;7;8;9;-6;-7;-8;-9 \right\}$.
Đáp án A.
