Google
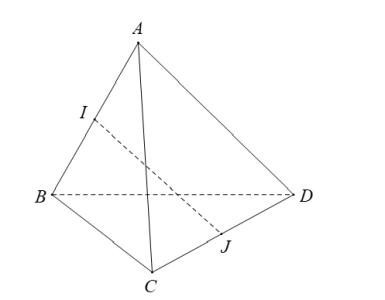
Câu hỏi: Cho tứ diện $A B C D$ có $A B=A C=A D$ và $\widehat{B A C}=\widehat{B A D}=60^{\circ}$. Gọi $I$ và $J$ lần lượt là trung điểm của $A B$ và $C D$
Hãy xác định góc giữa cặp véctơ $\overrightarrow{A B}$ và $\overrightarrow{I J}$.
A. $45^{\circ}$.
B. $90^{\circ}$.
C. $60^{\circ}$.
D. $120^{\circ}$.
Theo giả thiết $\triangle A B C ; \triangle A B D$ là hai tam giác đều và bằng nhau nên $C I \perp A B ; D I \perp A B$ từ đó suy ra $A B \perp(I C D) \Rightarrow A B \perp I J$. Do đó, góc giữa cặp véctơ $\overrightarrow{A B}$ và $\overrightarrow{I J}$ là $90^{\circ}$.
A. $45^{\circ}$.
B. $90^{\circ}$.
C. $60^{\circ}$.
D. $120^{\circ}$.
Đáp án B.