Google
Câu hỏi: Cho tham số $m\in \mathbb{R}$, khi bất phương trình ${{6}^{\sqrt{x}}}+{{2}^{\dfrac{1}{\sqrt{x}}}}+{{m}^{2}}-8<0$ có tập nghiệm là $S=\left( a ; b \right)$ hãy xác định $S$ sao cho $b-a$ đạt giá trị lớn nhất.
A. $S=\left( \dfrac{1}{4} ; \log _{2}^{2}6 \right)$.
B. $S=\left( \log _{6}^{2}2 ; 1 \right)$.
C. ${{S}_{0}}=\left( \dfrac{1}{9} ; 1 \right)$.
D. ${{S}_{0}}=\left( \dfrac{1}{4} ; 1 \right)$.
A. $S=\left( \dfrac{1}{4} ; \log _{2}^{2}6 \right)$.
B. $S=\left( \log _{6}^{2}2 ; 1 \right)$.
C. ${{S}_{0}}=\left( \dfrac{1}{9} ; 1 \right)$.
D. ${{S}_{0}}=\left( \dfrac{1}{4} ; 1 \right)$.
Ta có: ${{6}^{\sqrt{x}}}+{{2}^{\dfrac{1}{\sqrt{x}}}}+{{m}^{2}}-8\le 0 \left( 1 \right)$. Điều kiện: $x>0$. Đặt $t=\sqrt{x}$, điều kiện: $t>0$.
Bất phương trình trên thành: ${{6}^{t}}+{{2}^{\dfrac{1}{t}}}-8<-{{m}^{2}} \left( 2 \right)$.
Xét hàm số $f\left( t \right)={{6}^{t}}+{{2}^{\dfrac{1}{t}}}-8$ liên tục trên $(0 ; +\infty )$ có $f'\left( t \right)={{6}^{t}}\ln 6-\dfrac{1}{{{t}^{2}}}{{2}^{\dfrac{1}{t}}}\ln 2$.
$f''\left( t \right)={{6}^{t}}{{\ln }^{2}}6+\dfrac{\ln 2+2t}{{{t}^{4}}}{{2}^{\dfrac{1}{t}}}\ln 2>0 \forall t\in (0 ; +\infty )$ nên $f'\left( t \right)$ đồng biến trên $(0 ; +\infty )$.
Ta lại có $\underset{t\to {{0}^{+}}}{\mathop{\lim }} f'\left( t \right)=-\infty $ và $\underset{t\to +\infty }{\mathop{\lim }} f'\left( t \right)=+\infty $.
Suy ra có đúng một ${{t}_{0}}\in \left( 0 ; +\infty \right)$ sao cho $f'\left( {{t}_{0}} \right)=0$. Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy phương trình $f\left( t \right)=0$ có nhiều nhất là 2 nghiệm.
Mà $f\left( 1 \right)=f\left( {{\log }_{6}}2 \right)=0$ nên phương trình $f\left( t \right)=0$ có đúng 2 nghiệm là $t=1; t={{\log }_{6}}2 $.
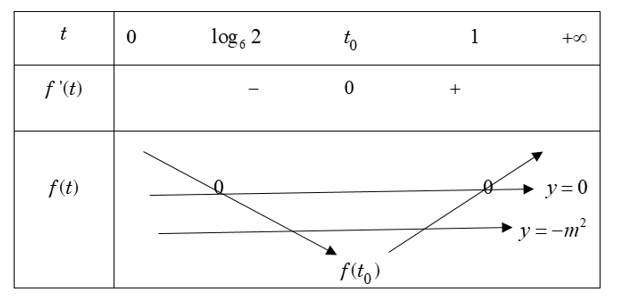$\left( 2 \right)$ có tập nghiệm $\left( \alpha ;\beta \right)$ sao cho $\beta -\alpha $ lớn nhất $\Leftrightarrow -{{m}^{2}}=0\Leftrightarrow m=0$.
Khi đó $\left( 2 \right)$ có tập nghiệm là $S'=\left( {{\log }_{6}}2 ; 1 \right)$ nên $\left( 1 \right)$ có tập nghiệm là $S=\left( \log _{6}^{2}2 ; 1 \right)$.
Bất phương trình trên thành: ${{6}^{t}}+{{2}^{\dfrac{1}{t}}}-8<-{{m}^{2}} \left( 2 \right)$.
Xét hàm số $f\left( t \right)={{6}^{t}}+{{2}^{\dfrac{1}{t}}}-8$ liên tục trên $(0 ; +\infty )$ có $f'\left( t \right)={{6}^{t}}\ln 6-\dfrac{1}{{{t}^{2}}}{{2}^{\dfrac{1}{t}}}\ln 2$.
$f''\left( t \right)={{6}^{t}}{{\ln }^{2}}6+\dfrac{\ln 2+2t}{{{t}^{4}}}{{2}^{\dfrac{1}{t}}}\ln 2>0 \forall t\in (0 ; +\infty )$ nên $f'\left( t \right)$ đồng biến trên $(0 ; +\infty )$.
Ta lại có $\underset{t\to {{0}^{+}}}{\mathop{\lim }} f'\left( t \right)=-\infty $ và $\underset{t\to +\infty }{\mathop{\lim }} f'\left( t \right)=+\infty $.
Suy ra có đúng một ${{t}_{0}}\in \left( 0 ; +\infty \right)$ sao cho $f'\left( {{t}_{0}} \right)=0$. Bảng biến thiên:
Mà $f\left( 1 \right)=f\left( {{\log }_{6}}2 \right)=0$ nên phương trình $f\left( t \right)=0$ có đúng 2 nghiệm là $t=1; t={{\log }_{6}}2 $.
Khi đó $\left( 2 \right)$ có tập nghiệm là $S'=\left( {{\log }_{6}}2 ; 1 \right)$ nên $\left( 1 \right)$ có tập nghiệm là $S=\left( \log _{6}^{2}2 ; 1 \right)$.
Đáp án B.