Google
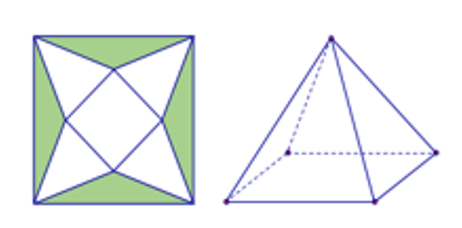
Câu hỏi: Cho một tấm tôn hình vuông cạnh $\sqrt{2}$ như hình vẽ dưới đây. người ta trách phần tô đậm của tấm tôn rồi gặp lại thành một hình chóp tứ giác đều và có cạnh đáy bằng $x$ sao cho 4 đỉnh của hình vuông ghép lại thành đỉnh của hình chóp. Khối chấp nhận được có thể tích lớn nhất bằng
A. $\dfrac{16\sqrt{5}}{375}$.
B. $\dfrac{\sqrt{3}}{18}$.
C. $\dfrac{4\sqrt{3}}{81}$.
D. $\dfrac{9\sqrt{2}}{128}$.
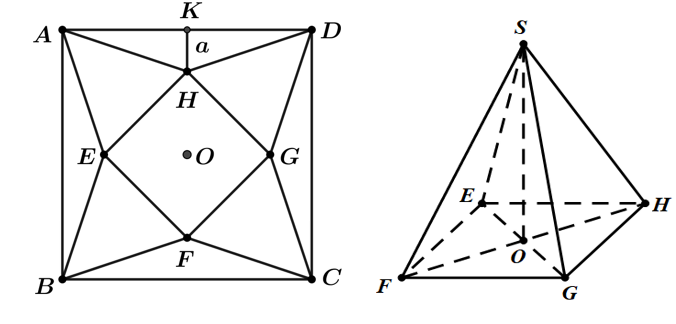Gọi $K$ là trung điểm $AD$, đặt $HK=a,\ 0<a<\dfrac{\sqrt{2}}{2}$.
Ta có $EF=FG=GH=HE=OH\sqrt{2}=\left( \dfrac{\sqrt{2}}{2}-a \right)\sqrt{2}=1-a\sqrt{2},\ HD=\sqrt{{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{a}^{2}}}$.
Suy ra $SO=\sqrt{S{{H}^{2}}-O{{H}^{2}}}=\sqrt{H{{D}^{2}}-O{{H}^{2}}}=\sqrt{{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{a}^{2}}-{{\left( \dfrac{\sqrt{2}}{2}-a \right)}^{2}}}=\sqrt{\sqrt{2}a}.$
Ta có $V=\dfrac{1}{3}.{{S}_{EFGH}}.SO=\dfrac{1}{3}{{\left( 1-a\sqrt{2} \right)}^{2}}\sqrt{\sqrt{2}a}$.
Đặt $t=1-a\sqrt{2}\Rightarrow a\sqrt{2}=1-t$ và $0<t<1$, ta có
$V=\dfrac{1}{3}{{t}^{2}}\sqrt{1-t}=\dfrac{1}{3}\sqrt{{{t}^{4}}\left( 1-t \right)}=\dfrac{1}{3}\sqrt{{{4}^{4}}.\dfrac{t}{4}.\dfrac{t}{4}.\dfrac{t}{4}.\dfrac{t}{4}.\left( 1-t \right)}\le \dfrac{16}{3}\sqrt{{{\left( \dfrac{\dfrac{t}{4}+\dfrac{t}{4}+\dfrac{t}{4}+\dfrac{t}{4}+(1-t)}{5} \right)}^{5}}}$.
Ta có $\max V=\dfrac{16\sqrt{5}}{375}$ khi $\dfrac{t}{4}=1-t\Leftrightarrow t=\dfrac{4}{5}$.
B. $\dfrac{\sqrt{3}}{18}$.
C. $\dfrac{4\sqrt{3}}{81}$.
D. $\dfrac{9\sqrt{2}}{128}$.
Ta có $EF=FG=GH=HE=OH\sqrt{2}=\left( \dfrac{\sqrt{2}}{2}-a \right)\sqrt{2}=1-a\sqrt{2},\ HD=\sqrt{{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{a}^{2}}}$.
Suy ra $SO=\sqrt{S{{H}^{2}}-O{{H}^{2}}}=\sqrt{H{{D}^{2}}-O{{H}^{2}}}=\sqrt{{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{a}^{2}}-{{\left( \dfrac{\sqrt{2}}{2}-a \right)}^{2}}}=\sqrt{\sqrt{2}a}.$
Ta có $V=\dfrac{1}{3}.{{S}_{EFGH}}.SO=\dfrac{1}{3}{{\left( 1-a\sqrt{2} \right)}^{2}}\sqrt{\sqrt{2}a}$.
Đặt $t=1-a\sqrt{2}\Rightarrow a\sqrt{2}=1-t$ và $0<t<1$, ta có
$V=\dfrac{1}{3}{{t}^{2}}\sqrt{1-t}=\dfrac{1}{3}\sqrt{{{t}^{4}}\left( 1-t \right)}=\dfrac{1}{3}\sqrt{{{4}^{4}}.\dfrac{t}{4}.\dfrac{t}{4}.\dfrac{t}{4}.\dfrac{t}{4}.\left( 1-t \right)}\le \dfrac{16}{3}\sqrt{{{\left( \dfrac{\dfrac{t}{4}+\dfrac{t}{4}+\dfrac{t}{4}+\dfrac{t}{4}+(1-t)}{5} \right)}^{5}}}$.
(Áp dụng bất đẳng thức AM – GM cho 5 số dương)
Suy ra $V\le \dfrac{16}{3}\sqrt{{{\left( \dfrac{1}{5} \right)}^{5}}}=\dfrac{16}{3}{{\left( \dfrac{1}{5} \right)}^{2}}\sqrt{\dfrac{1}{5}}=\dfrac{16}{75}.\dfrac{\sqrt{5}}{5}=\dfrac{16\sqrt{5}}{375}$.Ta có $\max V=\dfrac{16\sqrt{5}}{375}$ khi $\dfrac{t}{4}=1-t\Leftrightarrow t=\dfrac{4}{5}$.
Đáp án A.
