Google
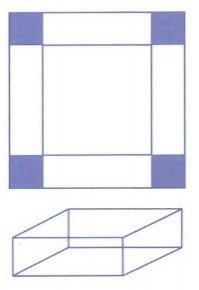
Câu hỏi: Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốm góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Giá trị của x để hộp nhận được có thể tích lớn nhất là
A. x = 6.
B. x = 3.
C. x = 2.
D. x = 4.
A. x = 6.
B. x = 3.
C. x = 2.
D. x = 4.
Ta có : h = x (cm) là đường cao hình hộp.
Vì tấm nhôm được gấp lại tại thành hình hộp nên cạnh đáy của hình hộp là : 12 – 2x (cm)
Diện tích đáy hình hộp $S={{\left( 12-2x \right)}^{2}}\left( c{{m}^{2}} \right)$. Ta có : $\left\{ \begin{aligned}
& x>0 \\
& 12-2x>0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x>0 \\
& x<6 \\
\end{aligned} \right.\Leftrightarrow x\in \left( 0;6 \right)$
Thể tích của hình hộp là : $V=S.h=x.{{\left( 12-2\text{x} \right)}^{2}}$. Xét hàm số : $y=x.{{\left( 12-2x \right)}^{2}}\forall x\in \left( 0;6 \right)$
Ta có : ${y}'={{\left( 12-2x \right)}^{2}}-4x\left( 12-2x \right)=\left( 12-2x \right)\left( 12-6x \right)$
${y}'=0\Leftrightarrow \left( 12-2x \right).\left( 12-6x \right)=0\Leftrightarrow x=2$ hoặc x = 6 (loại). Suy ra $y\left( 2 \right)=128$
Bảng biến thiên :
Vậy thể tích lớn nhất của hình hộp là $128\left( c{{m}^{3}} \right)$ khi x = 2 (cm).
Chú ý :
Có thể sử dụng table để tìm GTLN của $y=x.{{\left( 12-2\text{x} \right)}^{2}}\forall x\in \left( 0;6 \right)$ mà không cần vẽ bảng biến thiên như trên.
Vì tấm nhôm được gấp lại tại thành hình hộp nên cạnh đáy của hình hộp là : 12 – 2x (cm)
Diện tích đáy hình hộp $S={{\left( 12-2x \right)}^{2}}\left( c{{m}^{2}} \right)$. Ta có : $\left\{ \begin{aligned}
& x>0 \\
& 12-2x>0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x>0 \\
& x<6 \\
\end{aligned} \right.\Leftrightarrow x\in \left( 0;6 \right)$
Thể tích của hình hộp là : $V=S.h=x.{{\left( 12-2\text{x} \right)}^{2}}$. Xét hàm số : $y=x.{{\left( 12-2x \right)}^{2}}\forall x\in \left( 0;6 \right)$
Ta có : ${y}'={{\left( 12-2x \right)}^{2}}-4x\left( 12-2x \right)=\left( 12-2x \right)\left( 12-6x \right)$
${y}'=0\Leftrightarrow \left( 12-2x \right).\left( 12-6x \right)=0\Leftrightarrow x=2$ hoặc x = 6 (loại). Suy ra $y\left( 2 \right)=128$
Bảng biến thiên :
Chú ý :
Có thể sử dụng table để tìm GTLN của $y=x.{{\left( 12-2\text{x} \right)}^{2}}\forall x\in \left( 0;6 \right)$ mà không cần vẽ bảng biến thiên như trên.
Đáp án C.