Câu hỏi: Cho khối chóp $S.ABCD$ có đáy là hình vuông cạnh $2a$, tam giác $\Delta SAB$ vuông cân tại $S$, tam giác $\Delta SCD$ có $SC=SD=\dfrac{\sqrt{10}}{2}a$. Thể tích khối chóp đã cho bằng
A. $\dfrac{\sqrt{15}}{18}{{a}^{3}}$.
B. $\dfrac{\sqrt{15}}{12}{{a}^{3}}$.
C. $\dfrac{\sqrt{21}}{24}{{a}^{3}}$.
D. $\dfrac{\sqrt{15}}{6}{{a}^{3}}$.
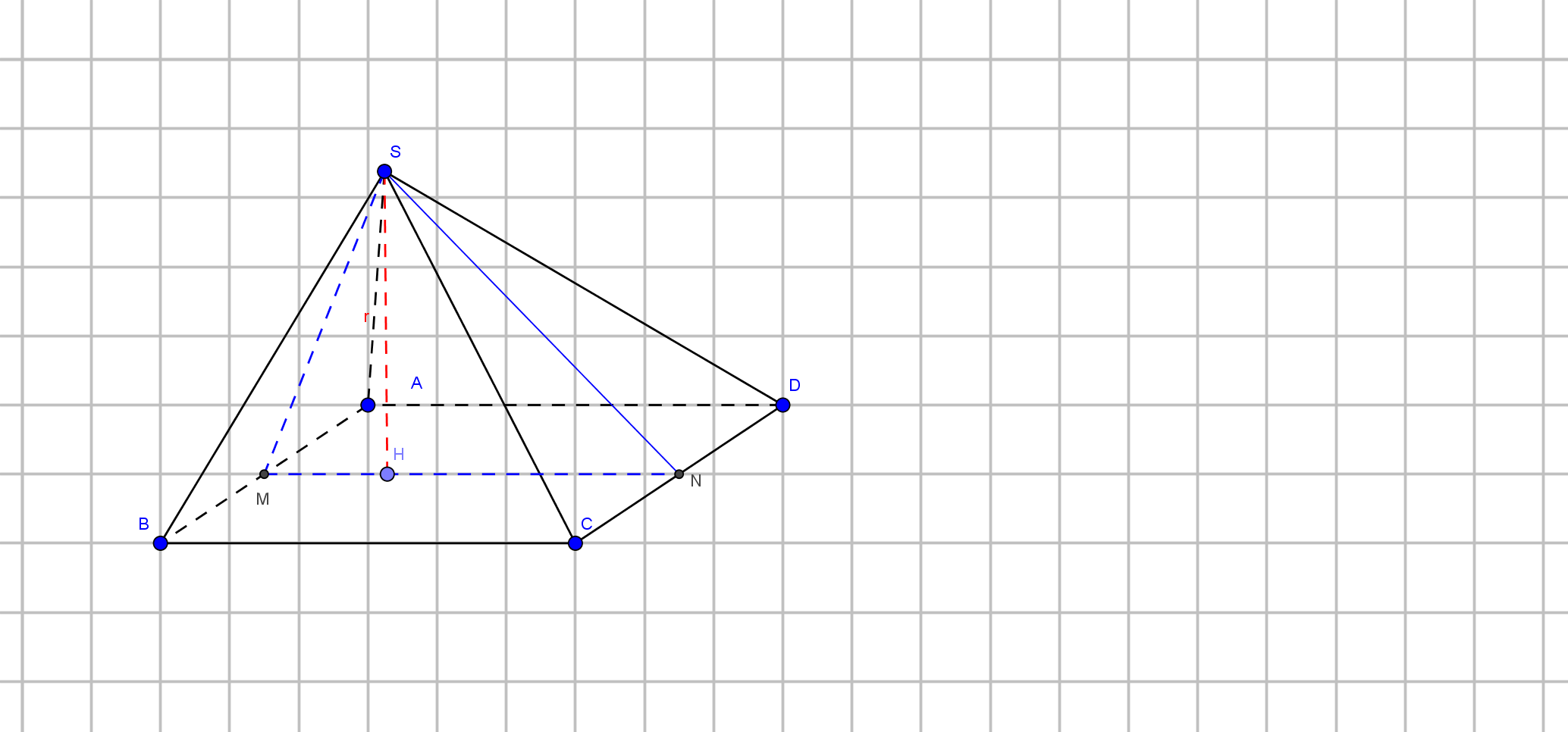 Gọi $M,N$ là trung điểm của $AB, CD$.
Gọi $M,N$ là trung điểm của $AB, CD$.
Gọi $H$ là chân đường cao của tam giác $\Delta SMN$.
Vì tam giác $\Delta SCD$ cân tại $S$ nên $SN\bot CD$.
Ta có:
$\left. \begin{aligned}
& CD\bot SN \\
& CD\bot MN \\
& SN,MN\subset \left( SMN \right) \\
& SN\cap MN=N \\
\end{aligned} \right\}\Rightarrow CD\bot \left( SMN \right)\Rightarrow CD\bot SH$
Mặt khác
$\left. \begin{aligned}
& SH\bot CD \\
& SH\bot MN \\
& CD,MN\subset \left( ABCD \right) \\
& CD\cap MN=N \\
\end{aligned} \right\}\Rightarrow SH\bot \left( ABCD \right)$
Vì tam giác $\Delta SAB$ vuông cân tại $S$ và $AB=2a$ nên $SM=\dfrac{AB}{2}=a$.
Xét tam giác $\Delta SNC$ vuông tại $N$.
$SN=\sqrt{S{{C}^{2}}-C{{N}^{2}}}=\sqrt{{{\left( \dfrac{\sqrt{10}}{2}a \right)}^{2}}-{{a}^{2}}}=\dfrac{a\sqrt{6}}{2}$.
$MN=AB=2a$
Nửa chu vi của tam giác $\Delta SMN$ là: $p=\dfrac{SM+MN+SN}{2}=\dfrac{\left( 6+\sqrt{6} \right).a}{4}$
$\Rightarrow {{S}_{\Delta SMN}}=\sqrt{p\left( p-SM \right).\left( p-MN \right).\left( p-SN \right)}=\dfrac{\sqrt{15}}{8}{{a}^{2}}$
Mặt khác: ${{S}_{\Delta SMN}}=\dfrac{1}{2}SH.MN\Rightarrow \dfrac{\sqrt{15}}{8}{{a}^{2}}=\dfrac{1}{2}SH.2a\Rightarrow SH=\dfrac{\sqrt{15}}{8}a$
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}{{S}_{ABCD}}.SH=\dfrac{1}{3}.{{\left( 2a \right)}^{2}}.\dfrac{\sqrt{15}}{8}a=\dfrac{\sqrt{15}{{a}^{3}}}{6}$.
A. $\dfrac{\sqrt{15}}{18}{{a}^{3}}$.
B. $\dfrac{\sqrt{15}}{12}{{a}^{3}}$.
C. $\dfrac{\sqrt{21}}{24}{{a}^{3}}$.
D. $\dfrac{\sqrt{15}}{6}{{a}^{3}}$.
Gọi $H$ là chân đường cao của tam giác $\Delta SMN$.
Vì tam giác $\Delta SCD$ cân tại $S$ nên $SN\bot CD$.
Ta có:
$\left. \begin{aligned}
& CD\bot SN \\
& CD\bot MN \\
& SN,MN\subset \left( SMN \right) \\
& SN\cap MN=N \\
\end{aligned} \right\}\Rightarrow CD\bot \left( SMN \right)\Rightarrow CD\bot SH$
Mặt khác
$\left. \begin{aligned}
& SH\bot CD \\
& SH\bot MN \\
& CD,MN\subset \left( ABCD \right) \\
& CD\cap MN=N \\
\end{aligned} \right\}\Rightarrow SH\bot \left( ABCD \right)$
Vì tam giác $\Delta SAB$ vuông cân tại $S$ và $AB=2a$ nên $SM=\dfrac{AB}{2}=a$.
Xét tam giác $\Delta SNC$ vuông tại $N$.
$SN=\sqrt{S{{C}^{2}}-C{{N}^{2}}}=\sqrt{{{\left( \dfrac{\sqrt{10}}{2}a \right)}^{2}}-{{a}^{2}}}=\dfrac{a\sqrt{6}}{2}$.
$MN=AB=2a$
Nửa chu vi của tam giác $\Delta SMN$ là: $p=\dfrac{SM+MN+SN}{2}=\dfrac{\left( 6+\sqrt{6} \right).a}{4}$
$\Rightarrow {{S}_{\Delta SMN}}=\sqrt{p\left( p-SM \right).\left( p-MN \right).\left( p-SN \right)}=\dfrac{\sqrt{15}}{8}{{a}^{2}}$
Mặt khác: ${{S}_{\Delta SMN}}=\dfrac{1}{2}SH.MN\Rightarrow \dfrac{\sqrt{15}}{8}{{a}^{2}}=\dfrac{1}{2}SH.2a\Rightarrow SH=\dfrac{\sqrt{15}}{8}a$
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}{{S}_{ABCD}}.SH=\dfrac{1}{3}.{{\left( 2a \right)}^{2}}.\dfrac{\sqrt{15}}{8}a=\dfrac{\sqrt{15}{{a}^{3}}}{6}$.
Đáp án D.