Google
Câu hỏi: Cho khối chóp $S.ABCD$ có đáy là hình bình hành $AB=3,AD=4$, $\widehat{BAD}=120{}^\circ $. Cạnh bên $SA=2\sqrt{3}$ và vuông góc với mặt phẳng $\left( ABCD \right)$. Gọi $M,N,P$ lần lượt là trung điểm các cạnh $SA,SD$ và $BC$, $\alpha $ là góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( MNP \right)$. Khẳng định nào sau đây là khẳng định đúng?
A. $\alpha \in \left( 0{}^\circ ;30{}^\circ \right)$.
B. $\alpha \in \left( 30{}^\circ ;45{}^\circ \right)$.
C. $\alpha \in \left( 45{}^\circ ;60{}^\circ \right)$.
D. $\alpha \in \left( 60{}^\circ ;90{}^\circ \right)$.
A. $\alpha \in \left( 0{}^\circ ;30{}^\circ \right)$.
B. $\alpha \in \left( 30{}^\circ ;45{}^\circ \right)$.
C. $\alpha \in \left( 45{}^\circ ;60{}^\circ \right)$.
D. $\alpha \in \left( 60{}^\circ ;90{}^\circ \right)$.
Cách 1:
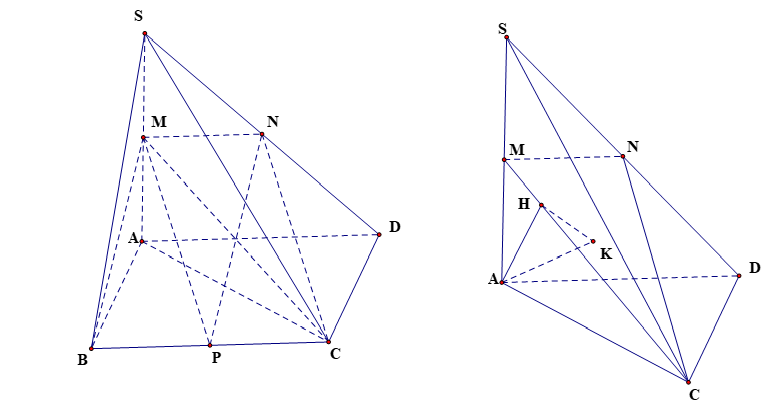Ta thấy $MN//BC$ nên $\left( MNP \right)\equiv \left( MNBC \right)$.
Ta có $\left( SAC \right)\cap \left( MNBC \right)=MC$.
Dựng $\left\{ \begin{aligned}
& AK\bot \left( MNBC \right) \\
& AH\bot MC \\
\end{aligned} \right.\Rightarrow \left( AHK \right)\bot MC $ $ \Rightarrow HK\bot MC$.
Do đó, góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( MNP \right)$ bằng góc $\widehat{AHK}$.
Ta có $AC=\sqrt{A{{D}^{2}}+C{{D}^{2}}-2AD.CD.\cos \text{60}{}^\circ }=\sqrt{13}$.
$SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\sqrt{25}=5$, $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{M}^{2}}}+\dfrac{1}{A{{C}^{2}}}\Rightarrow AH=\dfrac{\sqrt{39}}{4}$.
$MC=\sqrt{A{{M}^{2}}+A{{C}^{2}}}=\sqrt{16}=4$, $MN=\dfrac{AD}{2}=2$.
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=2\sqrt{7}$ ; $CN=\sqrt{\dfrac{S{{C}^{2}}+C{{D}^{2}}}{2}-\dfrac{S{{D}^{2}}}{4}}=\sqrt{10}$.
${{V}_{C.AMN}}=\dfrac{1}{3}{{S}_{AMN}}.d\left( C,\left( AMN \right) \right)=\dfrac{1}{3}\left( \dfrac{1}{2}.AM.MN \right).d\left( C,AD \right)$ $=\dfrac{1}{3}\left( \dfrac{1}{2}.\sqrt{3}.2 \right).3.\sin 60{}^\circ =\dfrac{3}{2}$.
${{S}_{CMN}}=\dfrac{\sqrt{39}}{2}$ $\Rightarrow AK=\dfrac{3{{V}_{A.CMN}}}{{{S}_{CMN}}}=\dfrac{3\sqrt{39}}{13}$.
Tam giác $AHK$ vuông tại $K$, suy ra $\sin \widehat{AHK}=\dfrac{AK}{AH}=\dfrac{12}{13}\Rightarrow \widehat{AHK}\approx 67{}^\circ 38'$
Cách 2:
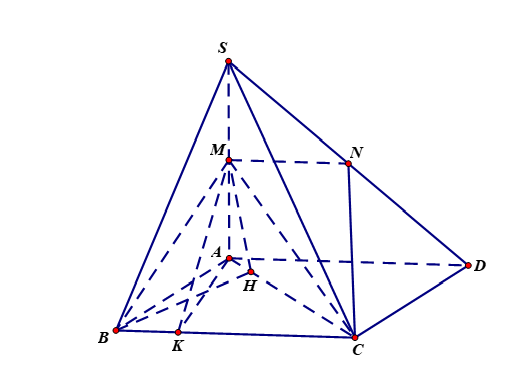Với mọi điểm $P\in BC$ ta có $\left( MNP \right)\equiv \left( BCNM \right)\equiv \left( MBC \right)$, do đó $\left( MNP,SAC \right)=\left( MBC,SAC \right)$
Gọi $H$ là hình chiếu của $B$ lên $AC$ thì $BH\bot \left( SAC \right)$ nên $\Delta MHC$ là hình chiếu của $\Delta MBC$ lên mp $\left( SAC \right)$, do đó $S\left( \Delta MHC \right)=S\left( \Delta MBC \right).\cos \alpha $ ; $\left( MBC,SAC \right)=\alpha $.
Gọi $K$ là hình chiếu của $A$ lên $BC$ thì $MK\bot BC$. Ta có $AK=AB.\sin \angle ABK=3.\sin {{60}^{0}}=\dfrac{3\sqrt{3}}{2}$ $\Rightarrow MK=\sqrt{M{{A}^{2}}+A{{K}^{2}}}=\dfrac{\sqrt{39}}{2}\Rightarrow S\left( \Delta MBC \right)=\dfrac{1}{2}BC.MK=\sqrt{39}$.
Ta có $KB=AB.\cos \angle ABK=\dfrac{3}{2}\Rightarrow KC=\dfrac{5}{2}$ $\Rightarrow AC=\sqrt{A{{K}^{2}}+K{{C}^{2}}}=\sqrt{13}\Rightarrow BH=\dfrac{BC.AK}{AC}=\dfrac{6\sqrt{39}}{13}$ $\Rightarrow CH=\sqrt{B{{C}^{2}}-B{{H}^{2}}}=\dfrac{10\sqrt{13}}{13}$ $\Rightarrow S\left( \Delta MHC \right)=\dfrac{1}{2}CH.MA=\dfrac{5\sqrt{39}}{13}$
Suy ra $\cos \alpha =\dfrac{S\left( \Delta MHC \right)}{S\left( \Delta MBC \right)}=\dfrac{5\sqrt{39}}{13\sqrt{39}}=\dfrac{5}{13}\Rightarrow \alpha \in \left( {{60}^{0}};{{90}^{0}} \right)$
Cách 3 :
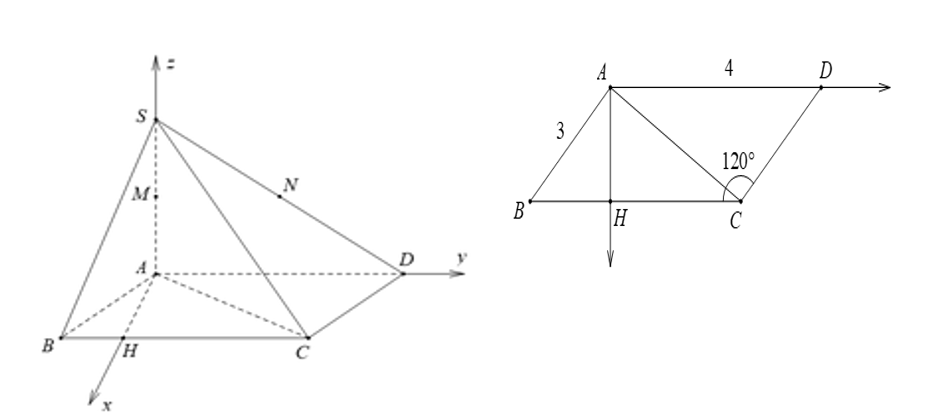
Hạ $AH\bot BC$, vì tam giác $ABH$ có $AB=3,$ góc $\widehat{BAH}={{30}^{\text{o}}}$ suy ra: $AH=\dfrac{3\sqrt{3}}{2};\ BH=\dfrac{3}{2}\Rightarrow CH=\dfrac{5}{2}$.
Gắn hệ trục tọa độ $\text{Ox}yz$ sao cho $O\equiv A\ ;H\in \text{Ox}\ \text{; D}\in \text{Oy}\ \text{;S}\in \text{Oz}$. Suy ra $A\left( 0;0;0 \right);\ H\left( \dfrac{3\sqrt{3}}{2};0;0 \right);\ D\left( 0;4;0 \right);\ S\left( 0;0;2\sqrt{3} \right)$ ; $B\left( \dfrac{3\sqrt{3}}{2};\dfrac{-3}{2};0 \right);\ C\left( \dfrac{3\sqrt{3}}{2};\dfrac{5}{2};0 \right);\ M\left( 0;0;\sqrt{3} \right);\ N\left( 0;2;\sqrt{3} \right);\ P\left( \dfrac{3\sqrt{3}}{2};\dfrac{1}{2};0 \right)$
Khi đó: $\overrightarrow{{{n}_{1}}}=\overrightarrow{{{n}_{\left( SAC \right)}}}=\left[ \overrightarrow{SA};\overrightarrow{AC} \right]=\left( 5\sqrt{3};-9;0 \right)$
$\overrightarrow{{{n}_{2}}}=\overrightarrow{{{n}_{\left( MNP \right)}}}=\left[ \overrightarrow{MP};\overrightarrow{MN} \right]=\left( 2\sqrt{3};0;3\sqrt{3} \right)$
Suy ra: $\cos \alpha =\dfrac{\left| \overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|.\left| \overrightarrow{{{n}_{2}}} \right|}=\dfrac{\left| 30+0+0 \right|}{\sqrt{156}.\sqrt{39}}=\dfrac{5}{13}.$
Vậy: $\alpha \in \left( {{60}^{o}};{{90}^{o}} \right)$.
Ta có $\left( SAC \right)\cap \left( MNBC \right)=MC$.
Dựng $\left\{ \begin{aligned}
& AK\bot \left( MNBC \right) \\
& AH\bot MC \\
\end{aligned} \right.\Rightarrow \left( AHK \right)\bot MC $ $ \Rightarrow HK\bot MC$.
Do đó, góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( MNP \right)$ bằng góc $\widehat{AHK}$.
Ta có $AC=\sqrt{A{{D}^{2}}+C{{D}^{2}}-2AD.CD.\cos \text{60}{}^\circ }=\sqrt{13}$.
$SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\sqrt{25}=5$, $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{M}^{2}}}+\dfrac{1}{A{{C}^{2}}}\Rightarrow AH=\dfrac{\sqrt{39}}{4}$.
$MC=\sqrt{A{{M}^{2}}+A{{C}^{2}}}=\sqrt{16}=4$, $MN=\dfrac{AD}{2}=2$.
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=2\sqrt{7}$ ; $CN=\sqrt{\dfrac{S{{C}^{2}}+C{{D}^{2}}}{2}-\dfrac{S{{D}^{2}}}{4}}=\sqrt{10}$.
${{V}_{C.AMN}}=\dfrac{1}{3}{{S}_{AMN}}.d\left( C,\left( AMN \right) \right)=\dfrac{1}{3}\left( \dfrac{1}{2}.AM.MN \right).d\left( C,AD \right)$ $=\dfrac{1}{3}\left( \dfrac{1}{2}.\sqrt{3}.2 \right).3.\sin 60{}^\circ =\dfrac{3}{2}$.
${{S}_{CMN}}=\dfrac{\sqrt{39}}{2}$ $\Rightarrow AK=\dfrac{3{{V}_{A.CMN}}}{{{S}_{CMN}}}=\dfrac{3\sqrt{39}}{13}$.
Tam giác $AHK$ vuông tại $K$, suy ra $\sin \widehat{AHK}=\dfrac{AK}{AH}=\dfrac{12}{13}\Rightarrow \widehat{AHK}\approx 67{}^\circ 38'$
Cách 2:
Gọi $H$ là hình chiếu của $B$ lên $AC$ thì $BH\bot \left( SAC \right)$ nên $\Delta MHC$ là hình chiếu của $\Delta MBC$ lên mp $\left( SAC \right)$, do đó $S\left( \Delta MHC \right)=S\left( \Delta MBC \right).\cos \alpha $ ; $\left( MBC,SAC \right)=\alpha $.
Gọi $K$ là hình chiếu của $A$ lên $BC$ thì $MK\bot BC$. Ta có $AK=AB.\sin \angle ABK=3.\sin {{60}^{0}}=\dfrac{3\sqrt{3}}{2}$ $\Rightarrow MK=\sqrt{M{{A}^{2}}+A{{K}^{2}}}=\dfrac{\sqrt{39}}{2}\Rightarrow S\left( \Delta MBC \right)=\dfrac{1}{2}BC.MK=\sqrt{39}$.
Ta có $KB=AB.\cos \angle ABK=\dfrac{3}{2}\Rightarrow KC=\dfrac{5}{2}$ $\Rightarrow AC=\sqrt{A{{K}^{2}}+K{{C}^{2}}}=\sqrt{13}\Rightarrow BH=\dfrac{BC.AK}{AC}=\dfrac{6\sqrt{39}}{13}$ $\Rightarrow CH=\sqrt{B{{C}^{2}}-B{{H}^{2}}}=\dfrac{10\sqrt{13}}{13}$ $\Rightarrow S\left( \Delta MHC \right)=\dfrac{1}{2}CH.MA=\dfrac{5\sqrt{39}}{13}$
Suy ra $\cos \alpha =\dfrac{S\left( \Delta MHC \right)}{S\left( \Delta MBC \right)}=\dfrac{5\sqrt{39}}{13\sqrt{39}}=\dfrac{5}{13}\Rightarrow \alpha \in \left( {{60}^{0}};{{90}^{0}} \right)$
Cách 3 :
Hạ $AH\bot BC$, vì tam giác $ABH$ có $AB=3,$ góc $\widehat{BAH}={{30}^{\text{o}}}$ suy ra: $AH=\dfrac{3\sqrt{3}}{2};\ BH=\dfrac{3}{2}\Rightarrow CH=\dfrac{5}{2}$.
Gắn hệ trục tọa độ $\text{Ox}yz$ sao cho $O\equiv A\ ;H\in \text{Ox}\ \text{; D}\in \text{Oy}\ \text{;S}\in \text{Oz}$. Suy ra $A\left( 0;0;0 \right);\ H\left( \dfrac{3\sqrt{3}}{2};0;0 \right);\ D\left( 0;4;0 \right);\ S\left( 0;0;2\sqrt{3} \right)$ ; $B\left( \dfrac{3\sqrt{3}}{2};\dfrac{-3}{2};0 \right);\ C\left( \dfrac{3\sqrt{3}}{2};\dfrac{5}{2};0 \right);\ M\left( 0;0;\sqrt{3} \right);\ N\left( 0;2;\sqrt{3} \right);\ P\left( \dfrac{3\sqrt{3}}{2};\dfrac{1}{2};0 \right)$
Khi đó: $\overrightarrow{{{n}_{1}}}=\overrightarrow{{{n}_{\left( SAC \right)}}}=\left[ \overrightarrow{SA};\overrightarrow{AC} \right]=\left( 5\sqrt{3};-9;0 \right)$
$\overrightarrow{{{n}_{2}}}=\overrightarrow{{{n}_{\left( MNP \right)}}}=\left[ \overrightarrow{MP};\overrightarrow{MN} \right]=\left( 2\sqrt{3};0;3\sqrt{3} \right)$
Suy ra: $\cos \alpha =\dfrac{\left| \overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|.\left| \overrightarrow{{{n}_{2}}} \right|}=\dfrac{\left| 30+0+0 \right|}{\sqrt{156}.\sqrt{39}}=\dfrac{5}{13}.$
Vậy: $\alpha \in \left( {{60}^{o}};{{90}^{o}} \right)$.
Đáp án D.