Google
Câu hỏi: Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$, $AB=a$, $BC=2a$ và $\widehat{ABC}={{60}^{0}}$. Hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $\left( ABCD \right)$ là điểm $O$. Biết hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ vuông góc với nhau, thể tích của khối chóp đã cho bằng
A. $\dfrac{\sqrt{21}{{a}^{3}}}{6}$.
B. $\dfrac{\sqrt{3}{{a}^{3}}}{6}$.
C. $\dfrac{\sqrt{3}{{a}^{3}}}{3}$.
D. $\dfrac{{{a}^{3}}}{2}$.
Diện tích hình bình hành $ABCD$ là: ${{S}_{ABCD}}=2{{S}_{\Delta ABC}}=AB.BC.\sin \widehat{ABC}=a.2a.\sin {{60}^{0}}=\sqrt{3}{{a}^{2}}$
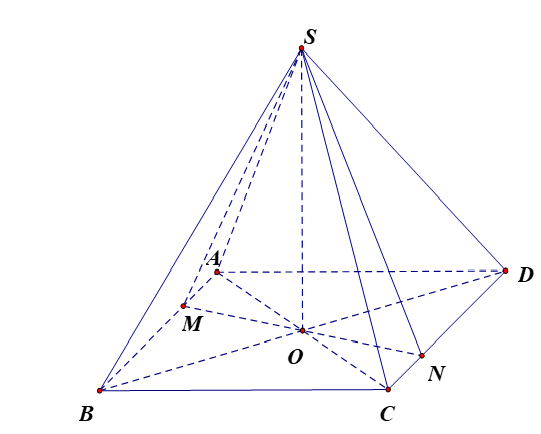
Trong mặt phẳng $\left( ABCD \right)$, qua $O$ kẻ đường thẳng vuông góc với $AB,\ CD$ cắt $AB,\ CD$ lần lượt tại $M,\ N$. Suy ra góc giữa hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ bằng góc giữa $SM,\ SN$. Mà hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ vuông góc với nhau nên $SM,\ SN$ vuông góc Do đó tam giác $SMN$ vuông tại $S$.
Ta có ${{S}_{\Delta OAB}}=\dfrac{1}{4}{{S}_{ABCD}}=\dfrac{\sqrt{3}{{a}^{2}}}{4}$ $\Rightarrow OM=\dfrac{2{{S}_{\Delta OAB}}}{AB}=\dfrac{\dfrac{\sqrt{3}{{a}^{2}}}{2}}{a}=\dfrac{\sqrt{3}a}{2}\Rightarrow MN=\sqrt{3}a$.
Tam giác $SMN$ vuông tại $S$ và $O$ là trung điểm $MN$ nên $SO=\dfrac{1}{2}MN=\dfrac{\sqrt{3}a}{2}$.
Vậy thể tích khối chóp $S.ABCD$ bằng: $V=\dfrac{1}{3}{{S}_{S.ABCD}}.SO=\dfrac{1}{3}.\sqrt{3}{{a}^{2}}.\dfrac{\sqrt{3}a}{2}=\dfrac{{{a}^{3}}}{2}.$
A. $\dfrac{\sqrt{21}{{a}^{3}}}{6}$.
B. $\dfrac{\sqrt{3}{{a}^{3}}}{6}$.
C. $\dfrac{\sqrt{3}{{a}^{3}}}{3}$.
D. $\dfrac{{{a}^{3}}}{2}$.
Trong mặt phẳng $\left( ABCD \right)$, qua $O$ kẻ đường thẳng vuông góc với $AB,\ CD$ cắt $AB,\ CD$ lần lượt tại $M,\ N$. Suy ra góc giữa hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ bằng góc giữa $SM,\ SN$. Mà hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ vuông góc với nhau nên $SM,\ SN$ vuông góc Do đó tam giác $SMN$ vuông tại $S$.
Ta có ${{S}_{\Delta OAB}}=\dfrac{1}{4}{{S}_{ABCD}}=\dfrac{\sqrt{3}{{a}^{2}}}{4}$ $\Rightarrow OM=\dfrac{2{{S}_{\Delta OAB}}}{AB}=\dfrac{\dfrac{\sqrt{3}{{a}^{2}}}{2}}{a}=\dfrac{\sqrt{3}a}{2}\Rightarrow MN=\sqrt{3}a$.
Tam giác $SMN$ vuông tại $S$ và $O$ là trung điểm $MN$ nên $SO=\dfrac{1}{2}MN=\dfrac{\sqrt{3}a}{2}$.
Vậy thể tích khối chóp $S.ABCD$ bằng: $V=\dfrac{1}{3}{{S}_{S.ABCD}}.SO=\dfrac{1}{3}.\sqrt{3}{{a}^{2}}.\dfrac{\sqrt{3}a}{2}=\dfrac{{{a}^{3}}}{2}.$
Đáp án D.