Google
Câu hỏi: Cho hình trụ có bán kính $R$ và chiều cao $\sqrt{3}R$. Hai điểm $A$, $B$ lần lượt nằm trên hai đường tròn đáy sao cho góc giữa $AB$ và trục $d$ của hình trụ bằng $30{}^\circ $. Tính khoảng cách giữa $AB$ và trục của hình trụ.
A. $d\left( AB,d \right)=\dfrac{R}{2}$.
B. $d\left( AB,d \right)=R$.
C. $d\left( AB,d \right)=R\sqrt{3}$.
D. $d\left( AB,d \right)=\dfrac{R\sqrt{3}}{2}$.
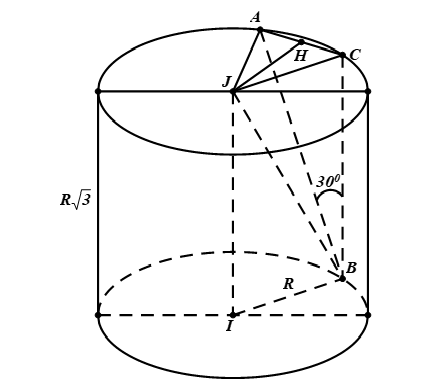Gọi $I$, $J$ là tâm của hai đáy.
Từ $B$ kẻ đường thẳng song song với trục $d$ của hình trụ, cắt đường tròn đáy kia tại $C$. Khi đó, $\left( AB,d \right)$ $=$ $\left( AB,BC \right)$ $=\widehat{ABC}$. Suy ra $\widehat{ABC}=30{}^\circ $.
Xét tam giác $ABC$ vuông tại $C$, ta có:
$\tan \widehat{ABC}=\dfrac{AC}{CB}$ $\Rightarrow $ $AC$ $=$ $CB.\tan \widehat{ABC}$ $=$ $R\sqrt{3}.\tan 30{}^\circ $ $=$ $R\sqrt{3}.\dfrac{1}{\sqrt{3}}$ $=$ $R$.
Lại có $d\text{//}\left( ABC \right)$ và $\left( ABC \right)\supset AB$ nên $d\left( d,AB \right)$ $=d\left( d,\left( ABC \right) \right)$ $=d\left( J,\left( ABC \right) \right)$.
Kẻ $JH\bot AC$, $H\in AC$. Vì $BC\bot JH$ nên $JH\bot \left( ABC \right)$. Suy ra $d\left( J,\left( ABC \right) \right)=JH$.
Xét tam giác $JAC$ ta thấy $JA=JC=AC=R$ nên $JAC$ là tam giác đều cạnh $R$. Khi đó chiều cao là $JH=\dfrac{R\sqrt{3}}{2}$. Vậy $d\left( d,AB \right)=\dfrac{R\sqrt{3}}{2}$.
A. $d\left( AB,d \right)=\dfrac{R}{2}$.
B. $d\left( AB,d \right)=R$.
C. $d\left( AB,d \right)=R\sqrt{3}$.
D. $d\left( AB,d \right)=\dfrac{R\sqrt{3}}{2}$.
Từ $B$ kẻ đường thẳng song song với trục $d$ của hình trụ, cắt đường tròn đáy kia tại $C$. Khi đó, $\left( AB,d \right)$ $=$ $\left( AB,BC \right)$ $=\widehat{ABC}$. Suy ra $\widehat{ABC}=30{}^\circ $.
Xét tam giác $ABC$ vuông tại $C$, ta có:
$\tan \widehat{ABC}=\dfrac{AC}{CB}$ $\Rightarrow $ $AC$ $=$ $CB.\tan \widehat{ABC}$ $=$ $R\sqrt{3}.\tan 30{}^\circ $ $=$ $R\sqrt{3}.\dfrac{1}{\sqrt{3}}$ $=$ $R$.
Lại có $d\text{//}\left( ABC \right)$ và $\left( ABC \right)\supset AB$ nên $d\left( d,AB \right)$ $=d\left( d,\left( ABC \right) \right)$ $=d\left( J,\left( ABC \right) \right)$.
Kẻ $JH\bot AC$, $H\in AC$. Vì $BC\bot JH$ nên $JH\bot \left( ABC \right)$. Suy ra $d\left( J,\left( ABC \right) \right)=JH$.
Xét tam giác $JAC$ ta thấy $JA=JC=AC=R$ nên $JAC$ là tam giác đều cạnh $R$. Khi đó chiều cao là $JH=\dfrac{R\sqrt{3}}{2}$. Vậy $d\left( d,AB \right)=\dfrac{R\sqrt{3}}{2}$.
Đáp án D.