Google
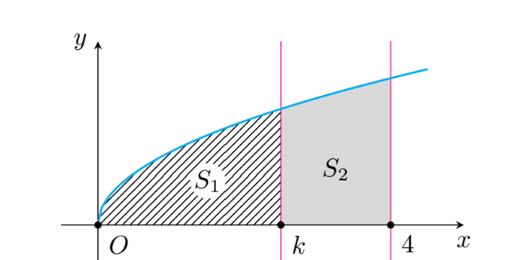
Câu hỏi: Cho hình thang cong $\left( H \right)$ giới hạn bởi các đường $y=\sqrt{x}, y=0, x=0, x=4$. Đường thẳng $x=k \left( 0<k<4 \right)$ chia hình $\left( H \right)$ thành hai phần có diện tích là ${{S}_{1}}$ và ${{S}_{2}}$ như hình vẽ. Để ${{S}_{1}}=4{{S}_{2}}$ thì giá trị $k$ thuộc khoảng nào sau đây?
A. $\left( 3,1; 3,3 \right)\cdot $
B. $\left( 3,7; 3,9 \right)\cdot $
C. $\left( 3,3; 3,5 \right)\cdot $
D. $\left( 3,5; 3,7 \right)\cdot $
B. $\left( 3,7; 3,9 \right)\cdot $
C. $\left( 3,3; 3,5 \right)\cdot $
D. $\left( 3,5; 3,7 \right)\cdot $
${{S}_{1}}={{\int\limits_{0}^{k}{\left( \sqrt{x} \right)\text{d}x={{\left. \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right|}^{k}}}}_{0}}=\dfrac{2}{3}{{k}^{\dfrac{3}{2}}}.$ ${{S}_{2}}={{\int\limits_{k}^{4}{\left( \sqrt{x} \right)\text{d}x={{\left. \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right|}^{4}}}}_{k}}=\dfrac{2}{3}{{.4}^{\dfrac{3}{2}}}-\dfrac{2}{3}.{{k}^{\dfrac{3}{2}}}.$
Suy ra ${{S}_{1}}=4{{S}_{2}}\Leftrightarrow \dfrac{2}{3}{{k}^{\dfrac{3}{2}}}=4\left[ \dfrac{2}{3}{{.4}^{\dfrac{3}{2}}}-\dfrac{2}{3}.{{k}^{\dfrac{3}{2}}} \right]\Leftrightarrow k\approx 3.447$.
Suy ra ${{S}_{1}}=4{{S}_{2}}\Leftrightarrow \dfrac{2}{3}{{k}^{\dfrac{3}{2}}}=4\left[ \dfrac{2}{3}{{.4}^{\dfrac{3}{2}}}-\dfrac{2}{3}.{{k}^{\dfrac{3}{2}}} \right]\Leftrightarrow k\approx 3.447$.
Đáp án C.