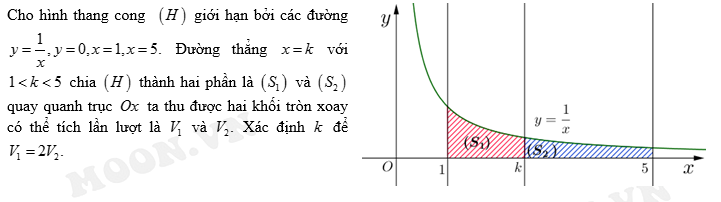
Câu hỏi: Cho hình thang cong (H) giới hạn bởi các đường $y=\dfrac{1}{x}, y=0, x=1, x=5$. Đường thẳng $x=k$ với $1<k<5$ chia (H) thành hai phần là $\left( {{S}_{1}} \right)$ và $\left( {{S}_{2}} \right)$ quay quanh trục Ox ta thu được hai khối tròn xoay có thể tích lần lượt là ${{V}_{1}} v\grave{a} {{V}_{2}}$. Xác định k để ${{V}_{1}}=2{{V}_{2}}$
A. $k=\dfrac{5}{3}$
B. $k=\dfrac{15}{7}$
C. $k=\ln 5$
D. $k=\sqrt[3]{25}$

A. $k=\dfrac{5}{3}$
B. $k=\dfrac{15}{7}$
C. $k=\ln 5$
D. $k=\sqrt[3]{25}$
Ta có: $\int{\dfrac{dx}{{{x}^{2}}}=-\dfrac{1}{x}=F\left( x \right)\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{\pi \int\limits_{1}^{k}{{{\left( \dfrac{1}{x} \right)}^{2}}dx}}{\pi \int\limits_{k}^{5}{{{\left( \dfrac{1}{x} \right)}^{2}}dx}}=\dfrac{F\left( k \right)-F\left( 1 \right)}{F\left( 5 \right)-F\left( k \right)}=2\Leftrightarrow k=\dfrac{15}{7}}$. Chọn B
Đáp án B.