Google
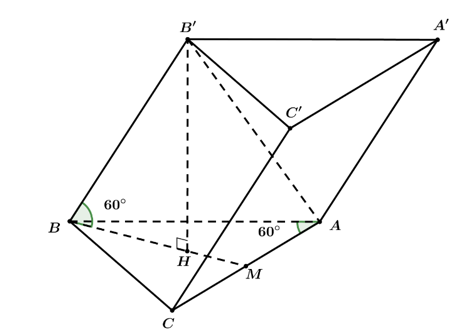
Câu hỏi: Cho hình lăng trụ tam giác $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$ có $B B^{\prime}=a$, góc giữa đường thẳng $B B^{\prime}$ và mặt phẳng $(A B C)$ bằng $60^{\circ}, \triangle A B C$ vuông tại $C$ và góc $B A C$ bằng $60^{\circ}$. Hình chiếu vuông góc của $B^{\prime}$ lên mặt phẳng $(A B C)$ trùng với trọng tâm của $\triangle A B C$. Thể tích của khối tứ diện $A^{\prime} . A B C$ là:
A. $\dfrac{3 a^3}{208}$.
B. $\dfrac{9 a^3}{200}$.
C. $\dfrac{a^3}{108}$.
D. $\dfrac{9 a^3}{108}$.
Thể tích khối tứ diện $V_{A \cdot A B C}=\dfrac{1}{3} B \cdot h=S_{A B C} \cdot h$.
Gọi $H$ là hình chiếu của $B^{\prime}$ lên mặt phẳng $(A B C)$, vậy $h=B^{\prime} H$.
Xét $\Delta B^{\prime} H B$ vuông tại $H$ : $\sin 60^{\circ}=\dfrac{B^{\prime} H}{B B^{\prime}} \Rightarrow B^{\prime} H=\dfrac{a \sqrt{3}}{2}, \cos 60^{\circ}=\dfrac{B H}{B B^{\prime}} \Rightarrow B H=\dfrac{1}{2} a$.
Gọi $M$ là trung điểm của $A C$, ta có $B H=\dfrac{2}{3} B M \Rightarrow B M=\dfrac{3}{2} B H=\dfrac{3}{2} \cdot \dfrac{1}{2} a=\dfrac{3 a}{4}$.
Đặt $A C=x$, xét $\triangle A B C$ vuông tại $C$ ta có tan $60^{\circ}=\dfrac{B C}{A C} \Rightarrow B C=A C \cdot \sqrt{3}=x \sqrt{3}$.
Xét $\triangle B C M$ vuông tại $C$ :
Theo Pitago: $B M^2=B C^2+C M^2$
$\Rightarrow\left(\dfrac{3 a}{4}\right)^2=(x \sqrt{3})^2+\left(\dfrac{x}{2}\right)^2 \Rightarrow \dfrac{9 a^2}{16}=\dfrac{13 x^2}{4} \Rightarrow x^2=\dfrac{9 a^2}{13.4}$
$\Rightarrow x=\dfrac{3}{2 \sqrt{13}} a=\dfrac{3 a \sqrt{13}}{26}$.
Vậy $S_{A B C}=\dfrac{1}{2} \cdot C B \cdot C A=\dfrac{1}{2} \cdot \dfrac{3 a \sqrt{13} \cdot \sqrt{3}}{26} \cdot \dfrac{3 a \sqrt{13}}{26}=\dfrac{9 a^2 \cdot \sqrt{3}}{104}$.
Thể tích của khối tứ diện $V_{A \prime \cdot A B C}=\dfrac{1}{3} \cdot S_{A B C} \cdot B^{\prime} H=\dfrac{1}{3} \cdot \dfrac{9 a^2 \sqrt{3}}{104} \cdot \dfrac{a \sqrt{3}}{2}=\dfrac{9 a^3}{208}$.
A. $\dfrac{3 a^3}{208}$.
B. $\dfrac{9 a^3}{200}$.
C. $\dfrac{a^3}{108}$.
D. $\dfrac{9 a^3}{108}$.
Gọi $H$ là hình chiếu của $B^{\prime}$ lên mặt phẳng $(A B C)$, vậy $h=B^{\prime} H$.
Xét $\Delta B^{\prime} H B$ vuông tại $H$ : $\sin 60^{\circ}=\dfrac{B^{\prime} H}{B B^{\prime}} \Rightarrow B^{\prime} H=\dfrac{a \sqrt{3}}{2}, \cos 60^{\circ}=\dfrac{B H}{B B^{\prime}} \Rightarrow B H=\dfrac{1}{2} a$.
Gọi $M$ là trung điểm của $A C$, ta có $B H=\dfrac{2}{3} B M \Rightarrow B M=\dfrac{3}{2} B H=\dfrac{3}{2} \cdot \dfrac{1}{2} a=\dfrac{3 a}{4}$.
Đặt $A C=x$, xét $\triangle A B C$ vuông tại $C$ ta có tan $60^{\circ}=\dfrac{B C}{A C} \Rightarrow B C=A C \cdot \sqrt{3}=x \sqrt{3}$.
Xét $\triangle B C M$ vuông tại $C$ :
Theo Pitago: $B M^2=B C^2+C M^2$
$\Rightarrow\left(\dfrac{3 a}{4}\right)^2=(x \sqrt{3})^2+\left(\dfrac{x}{2}\right)^2 \Rightarrow \dfrac{9 a^2}{16}=\dfrac{13 x^2}{4} \Rightarrow x^2=\dfrac{9 a^2}{13.4}$
$\Rightarrow x=\dfrac{3}{2 \sqrt{13}} a=\dfrac{3 a \sqrt{13}}{26}$.
Vậy $S_{A B C}=\dfrac{1}{2} \cdot C B \cdot C A=\dfrac{1}{2} \cdot \dfrac{3 a \sqrt{13} \cdot \sqrt{3}}{26} \cdot \dfrac{3 a \sqrt{13}}{26}=\dfrac{9 a^2 \cdot \sqrt{3}}{104}$.
Thể tích của khối tứ diện $V_{A \prime \cdot A B C}=\dfrac{1}{3} \cdot S_{A B C} \cdot B^{\prime} H=\dfrac{1}{3} \cdot \dfrac{9 a^2 \sqrt{3}}{104} \cdot \dfrac{a \sqrt{3}}{2}=\dfrac{9 a^3}{208}$.
Đáp án A.