Google
Câu hỏi: Cho hình lăng trụ $ABC.{A}'{B}'{C}'$ có $A{A}'=a$, đáy $ABC$ là tam giác đều, hình chiếu vuông góc của điểm $A$ trên mặt phẳng $\left( {A}'{B}'{C}' \right)$ trùng với trọng tâm của tam giác ${A}'{B}'{C}'$. Mặt phẳng $\left( B{B}'{C}'C \right)$ tạo với mặt phẳng $\left( {A}'{B}'{C}' \right)$ góc $60{}^\circ $. Tính thể tích $V$ của khối lăng trụ $ABC.{A}'{B}'{C}'$.
A. $V=\dfrac{{{a}^{3}}}{8}$.
B. $V=\dfrac{27{{a}^{3}}}{32}$.
C. $V=\dfrac{3{{a}^{3}}}{32}$.
D. $V=\dfrac{9{{a}^{3}}}{32}$.
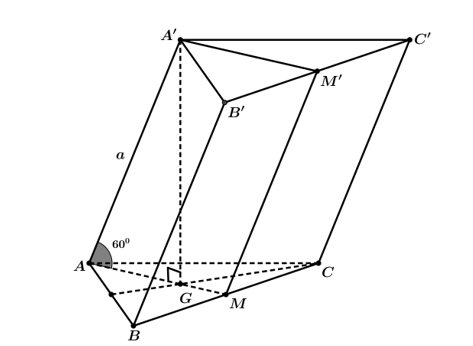Gọi $M$, ${M}'$ lần lượt là trung điểm của $BC$, ${B}'{C}'$ và $G$ là trọng tâm tam giác $ABC$.
Vì tam giác $ABC$ đều nên $BC\bot AM$. Mà $BC\bot {A}'G$ nên $BC\bot \left( A{A}'{M}'M \right)$.
Khi đó $\left( (ABC),(BC{C}'{B}' \right)=\left( AM,M{M}' \right)$.
Xét hình bình hành $A{A}'{M}'M$ có $\widehat{{A}'AM}$ là góc nhọn và bù với góc $\widehat{AM{M}'}$ nên
$\left( (ABC),(BC{C}'{B}' \right)=\left( AM,M{M}' \right)=180{}^\circ -\widehat{AM{M}'}=\widehat{{A}'AM}=60{}^\circ $.
Xét tam giác $A{A}'G$ vuông tại $G$, ta có ${A}'G=A{A}'.\sin 60{}^\circ =\dfrac{a\sqrt{3}}{2}$ ; $AG=A{A}'.\cos 60{}^\circ =\dfrac{a}{2}$,
$\Rightarrow AM=\dfrac{3}{2}AG=\dfrac{3a}{4}$.
Xét tam giác $ABM$ vuông tại $M$, ta có $\sin 60{}^\circ =\dfrac{AM}{AB}\Rightarrow AB=\dfrac{AM}{\sin 60{}^\circ }=\dfrac{a\sqrt{3}}{2}$.
$\Rightarrow {{S}_{\Delta ABC}}=\dfrac{1}{2}.AB.AC.\sin \widehat{BAC}=\dfrac{1}{2}.\dfrac{a\sqrt{3}}{2}.\dfrac{a\sqrt{3}}{2}.\sin 60{}^\circ =\dfrac{3{{a}^{2}}\sqrt{3}}{16}$.
Vậy ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.{A}'G=\dfrac{3{{a}^{2}}\sqrt{3}}{16}.\dfrac{a\sqrt{3}}{2}=\dfrac{9{{a}^{3}}}{32}$.
A. $V=\dfrac{{{a}^{3}}}{8}$.
B. $V=\dfrac{27{{a}^{3}}}{32}$.
C. $V=\dfrac{3{{a}^{3}}}{32}$.
D. $V=\dfrac{9{{a}^{3}}}{32}$.
Vì tam giác $ABC$ đều nên $BC\bot AM$. Mà $BC\bot {A}'G$ nên $BC\bot \left( A{A}'{M}'M \right)$.
Khi đó $\left( (ABC),(BC{C}'{B}' \right)=\left( AM,M{M}' \right)$.
Xét hình bình hành $A{A}'{M}'M$ có $\widehat{{A}'AM}$ là góc nhọn và bù với góc $\widehat{AM{M}'}$ nên
$\left( (ABC),(BC{C}'{B}' \right)=\left( AM,M{M}' \right)=180{}^\circ -\widehat{AM{M}'}=\widehat{{A}'AM}=60{}^\circ $.
Xét tam giác $A{A}'G$ vuông tại $G$, ta có ${A}'G=A{A}'.\sin 60{}^\circ =\dfrac{a\sqrt{3}}{2}$ ; $AG=A{A}'.\cos 60{}^\circ =\dfrac{a}{2}$,
$\Rightarrow AM=\dfrac{3}{2}AG=\dfrac{3a}{4}$.
Xét tam giác $ABM$ vuông tại $M$, ta có $\sin 60{}^\circ =\dfrac{AM}{AB}\Rightarrow AB=\dfrac{AM}{\sin 60{}^\circ }=\dfrac{a\sqrt{3}}{2}$.
$\Rightarrow {{S}_{\Delta ABC}}=\dfrac{1}{2}.AB.AC.\sin \widehat{BAC}=\dfrac{1}{2}.\dfrac{a\sqrt{3}}{2}.\dfrac{a\sqrt{3}}{2}.\sin 60{}^\circ =\dfrac{3{{a}^{2}}\sqrt{3}}{16}$.
Vậy ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.{A}'G=\dfrac{3{{a}^{2}}\sqrt{3}}{16}.\dfrac{a\sqrt{3}}{2}=\dfrac{9{{a}^{3}}}{32}$.
Đáp án D.