Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh $a$, mặt phẳng $\left( SAB \right)$ vuông góc với đáy và tam giác $SAB$ đều. Gọi $M$ là trung điểm của $SA$. Tính khoảng cách từ $M$ đến mặt phẳng $\left( SCD \right)$.
A. $\dfrac{a\sqrt{3}}{7}$.
B. $\dfrac{a\sqrt{3}}{14}$.
C. $\dfrac{a\sqrt{21}}{14}$.
D. $\dfrac{a\sqrt{21}}{7}$.
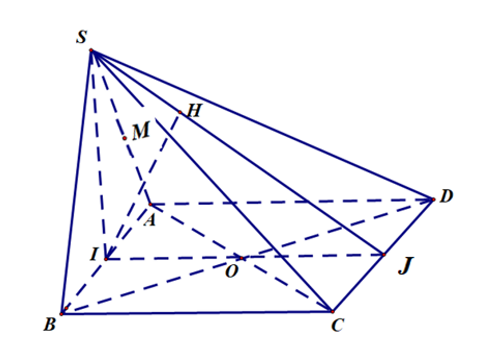sGọi $I$ là trung điểm $AB$.
Ta có $MA\cap \left( SCD \right)=S$ nên $d\left( M;\left( SCD \right) \right)=\dfrac{SM}{SA}d\left( A;\left( SCD \right) \right)=\dfrac{1}{2}d\left( A;\left( SCD \right) \right)$.
Mà $AI//CD\subset \left( SCD \right)$ nên $d\left( A;\left( SCD \right) \right)=d\left( I;\left( SCD \right) \right)$.
Gọi $J, H$ lần lượt là trung điểm $CD$ và hình chiếu của $I$ lên $SJ$.
Ta có $\left\{ \begin{aligned}
& CD\bot SI \\
& CD\bot IJ \\
\end{aligned} \right.\Rightarrow CD\bot IH $, mà $ SJ\bot IH $ nên $ IH\bot \left( SCD \right)$
Nên $d\left( I;\left( SCD \right) \right)=IH$.
$\Delta SIJ$ vuông tại $I$ nên $IH=\dfrac{SI.IJ}{\sqrt{S{{I}^{2}}+I{{J}^{2}}}}=\dfrac{a\dfrac{\sqrt{3}}{2}.a}{\sqrt{\dfrac{3}{4}{{a}^{2}}+{{a}^{2}}}}=a\dfrac{\sqrt{21}}{7}$.
Suy ra $d\left( M;\left( SCD \right) \right)=$ $a\dfrac{\sqrt{21}}{14}$.
B. $\dfrac{a\sqrt{3}}{14}$.
C. $\dfrac{a\sqrt{21}}{14}$.
D. $\dfrac{a\sqrt{21}}{7}$.
Ta có $MA\cap \left( SCD \right)=S$ nên $d\left( M;\left( SCD \right) \right)=\dfrac{SM}{SA}d\left( A;\left( SCD \right) \right)=\dfrac{1}{2}d\left( A;\left( SCD \right) \right)$.
Mà $AI//CD\subset \left( SCD \right)$ nên $d\left( A;\left( SCD \right) \right)=d\left( I;\left( SCD \right) \right)$.
Gọi $J, H$ lần lượt là trung điểm $CD$ và hình chiếu của $I$ lên $SJ$.
Ta có $\left\{ \begin{aligned}
& CD\bot SI \\
& CD\bot IJ \\
\end{aligned} \right.\Rightarrow CD\bot IH $, mà $ SJ\bot IH $ nên $ IH\bot \left( SCD \right)$
Nên $d\left( I;\left( SCD \right) \right)=IH$.
$\Delta SIJ$ vuông tại $I$ nên $IH=\dfrac{SI.IJ}{\sqrt{S{{I}^{2}}+I{{J}^{2}}}}=\dfrac{a\dfrac{\sqrt{3}}{2}.a}{\sqrt{\dfrac{3}{4}{{a}^{2}}+{{a}^{2}}}}=a\dfrac{\sqrt{21}}{7}$.
Suy ra $d\left( M;\left( SCD \right) \right)=$ $a\dfrac{\sqrt{21}}{14}$.
Đáp án C.
