Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật. Các mặt bên $\left( SAB \right)$ và $\left( SAD \right)$ vuông góc với đáy. Góc giữa mặt phẳng $\left( SCD \right)$ và $\left( ABCD \right)$ bằng $60{}^\circ ,$ $BC=a\sqrt{3}.$ Khoảng cách giữa hai đường thẳng $AB$ và $SC$ bằng
A. $\dfrac{3a}{2}$.
B. $\dfrac{6\sqrt{13}a}{13}$.
C. $\dfrac{a\sqrt{3}}{2}$.
D. $\dfrac{6\sqrt{5}a}{5}$.
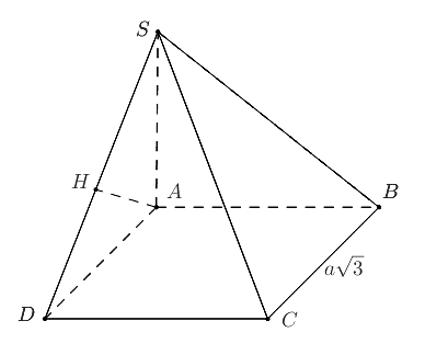$\left( SAB \right)$ và $\left( SAD \right)$ vuông góc với đáy nên $SA\bot \left( ABCD \right)$.
Ta có: $\left( SCD \right)\cap \left( ABCD \right)=CD$, $CD\bot \left( SAD \right)$, $\left( SAD \right)\cap \left( ABCD \right)=AD$,
$ \left( SAD \right)\cap \left( SCD \right)=SD$. Suy ra, góc giữa $\left( SCD \right)$ và $\left( ABCD \right)$ là $\widehat{SDA}$. Vậy $\widehat{SDA}=60{}^\circ $.
$\left\{ \begin{aligned}
& AB\text{//}\left( SCD \right) \\
& SC\subset \left( SCD \right) \\
\end{aligned} \right. $ $ \Rightarrow d\left( AB, SC \right)=d\left( AB, \left( SCD \right) \right)=d\left( A, \left( SCD \right) \right)$.
Gọi $H$ là hình chiếu của $A$ trên $SD$.
Ta có: $AH\bot SD; AH\bot CD$ do $CD\bot \left( SAD \right)$ $\Rightarrow AH\bot \left( SCD \right)$
$\Rightarrow d\left( A, \left( SCD \right) \right)=AH=AD\sin \widehat{ADS}=\dfrac{3a}{2}$. Vậy $d\left( AB, SC \right)=\dfrac{3a}{2}$.
A. $\dfrac{3a}{2}$.
B. $\dfrac{6\sqrt{13}a}{13}$.
C. $\dfrac{a\sqrt{3}}{2}$.
D. $\dfrac{6\sqrt{5}a}{5}$.
Ta có: $\left( SCD \right)\cap \left( ABCD \right)=CD$, $CD\bot \left( SAD \right)$, $\left( SAD \right)\cap \left( ABCD \right)=AD$,
$ \left( SAD \right)\cap \left( SCD \right)=SD$. Suy ra, góc giữa $\left( SCD \right)$ và $\left( ABCD \right)$ là $\widehat{SDA}$. Vậy $\widehat{SDA}=60{}^\circ $.
$\left\{ \begin{aligned}
& AB\text{//}\left( SCD \right) \\
& SC\subset \left( SCD \right) \\
\end{aligned} \right. $ $ \Rightarrow d\left( AB, SC \right)=d\left( AB, \left( SCD \right) \right)=d\left( A, \left( SCD \right) \right)$.
Gọi $H$ là hình chiếu của $A$ trên $SD$.
Ta có: $AH\bot SD; AH\bot CD$ do $CD\bot \left( SAD \right)$ $\Rightarrow AH\bot \left( SCD \right)$
$\Rightarrow d\left( A, \left( SCD \right) \right)=AH=AD\sin \widehat{ADS}=\dfrac{3a}{2}$. Vậy $d\left( AB, SC \right)=\dfrac{3a}{2}$.
Đáp án A.