Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình thang vuông tại $A$ ...

The Funny · 27/5/23

Câu hỏi: Cho hình chóp

S . A B C D

có đáy

A B C D

là hình thang vuông tại

A

và

D

,

S A

vuông góc với mặt phẳng đáy. Biết

A D = D C = a, A B = 2 a

. Khẳng định nào sau đây sai?
A.

(S B C) ⊥ (S A C)

.
B.

(S A D) ⊥ (S A B)

.
C.

(S C D) ⊥ (S A D)

.
D.

(S A C) ⊥ (S B D)

.

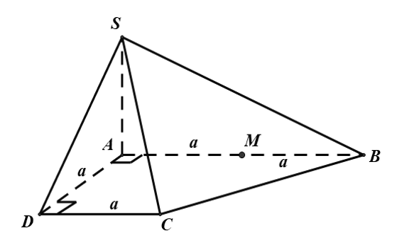Gọi

M

là trung điểm

A B

. Ta có

C M = M A = M B = a

. Suy ra

Δ A C B

vuông tại

C

.

{\begin{aligned} B C ⊥ A C \\ B C ⊥ S A \end{aligned} \Rightarrow B C ⊥ (S A C) \Rightarrow (S B C) ⊥ (S A C)

. Do đó phương án A đúng.

{\begin{aligned} A B ⊥ A D \\ A B ⊥ S A \end{aligned} \Rightarrow A B ⊥ (S A D) \Rightarrow (S A B) ⊥ (S A D)

. Do đó phương án B đúng.

{\begin{aligned} C D ⊥ A D \\ C D ⊥ S A \end{aligned} \Rightarrow C D ⊥ (S A D) \Rightarrow (S C D) ⊥ (S A D)

. Do đó phương án C đúng.

Đáp án D.

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A...