Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình chữ nhật...

The Funny · 20/6/23

Câu hỏi: Cho hình chóp

S . A B C D

có đáy

A B C D

là hình chữ nhật,

A B = a, A D = a \sqrt{3} .

Biết

S A ⊥ (A B C D)

và khoảng cách từ điểm

C

đến mặt phẳng

(S B D)

bằng

\frac{a \sqrt{21}}{7}

. Thể tích của khối chóp

S . A B C D

bằng
A.

\frac{2 \sqrt{3} a^{3}}{3}

.
B.

\frac{\sqrt{3} a^{3}}{3}

.
C.

\sqrt{3} a^{3}

.
D.

2 \sqrt{3} a^{3}

.

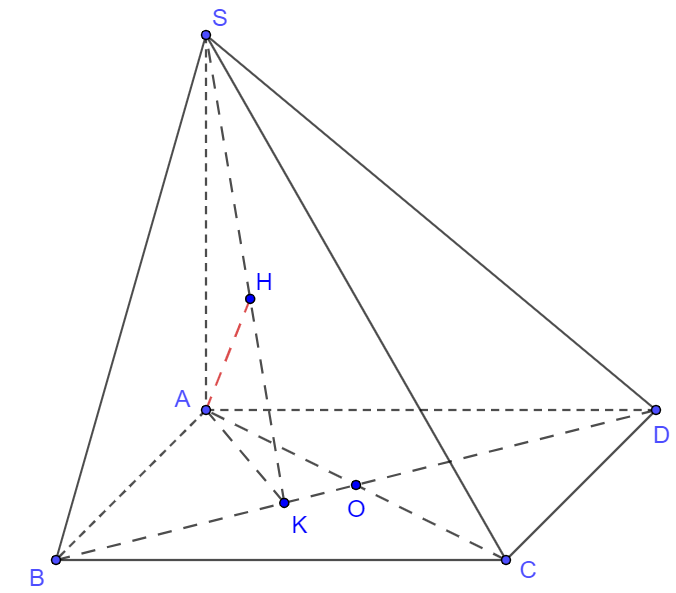Gọi

O

là giao điểm của

A C

và

B D,

kẻ

A K ⊥ B D (K \in B D), A H ⊥ S K (H \in S K)

.
Ta có:

A C \cap B D = {O} \Rightarrow d (C, (S B D)) = d (A, (S B D)) = \frac{a \sqrt{21}}{7}

Vì

{\begin{aligned} B D ⊥ A K \\ B D ⊥ S A \end{aligned} \Rightarrow B D ⊥ (S A K) \Rightarrow B D ⊥ A H

mà

A H ⊥ S K \Rightarrow A H ⊥ (S B D)

Nên

d (A, (S B D)) = A H = \frac{a \sqrt{21}}{7}

.
Xét tam giác

A B D

ta có:

\frac{1}{A K^{2}} = \frac{1}{A B^{2}} + \frac{1}{A D^{2}} = \frac{1}{a^{2}} + \frac{1}{3 a^{2}} = \frac{4}{3 a^{2}} \Rightarrow A K = \frac{a \sqrt{3}}{2} .

Xét tam giác

S A K

ta có:

\frac{1}{A H^{2}} = \frac{1}{S A^{2}} + \frac{1}{A K^{2}}

\Rightarrow \frac{1}{S A^{2}} = \frac{1}{A H^{2}} - \frac{1}{A K^{2}} = \frac{49}{21 a^{2}} - \frac{4}{3 a^{2}} = \frac{1}{a^{2}} \Rightarrow S A = a .

Vậy

V_{S . A B C D} = \frac{1}{3} S A . S_{A B C D} = \frac{1}{3} . a . a^{2} \sqrt{3} = \frac{a^{3} \sqrt{3}}{3} .

.

Đáp án B.

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật...