Câu hỏi: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AD=a,AB=2a$. Cạnh bên $SA$ vuông góc với đáy. Gọi $M,N$ lần lượt là trung điểm của $SB$ và $SD$. Tính khoảng cách d từ S đến mặt phẳng $\left( AMN \right)$.
A. $d=\dfrac{a\sqrt{6}}{3}$
B. $d=2a$
C. $d=\dfrac{3a}{2}$
D. $d=a\sqrt{5}$
A. $d=\dfrac{a\sqrt{6}}{3}$
B. $d=2a$
C. $d=\dfrac{3a}{2}$
D. $d=a\sqrt{5}$
Phương pháp giải:
- Tính thể tích chóp $S.ABCD$, sử dụng tỉ lệ thể tích Simpson tính thể tích khối chóp ${{V}_{S.AMN}}$.
- Sử dụng công thức ${{V}_{S.AMN}}=\dfrac{1}{3}d\left( S;\left( AMN \right) \right).{{S}_{AMN}}\Rightarrow d\left( S;\left( AMN \right) \right)=\dfrac{3{{V}_{S.AMN}}}{{{S}_{AMN}}}$.
- Sử dụng định lí Pytago, định lí đường trung tuyến trong tam giác vuông, tính chất đường trung bình của tam giác tính độ dài các cạnh của tam giác $AMN$, sau đó sử dụng công thức Hê-rông tính diện tích tam giác $AMN$ : ${{S}_{AMN}}=\sqrt{p\left( p-AM \right)\left( p-AN \right)\left( p-MN \right)}$ với p là nửa chu vi $\Delta AMN$.
Giải chi tiết:
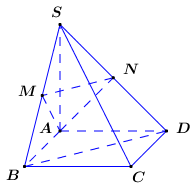
Áp dụng định lí Pytago trong các tam giác vuông $SAB,SAD,ABD$ ta có:
$SB=\sqrt{S{{A}^{2}}+A{{B}^{2}}}=\sqrt{4{{a}^{2}}+4{{a}^{2}}}=2\sqrt{2}a$
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=\sqrt{4{{a}^{2}}+{{a}^{2}}}=\sqrt{5}a$
$BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=\sqrt{4{{a}^{2}}+{{a}^{2}}}=\sqrt{5}a$
Khi đó ta có $AM=\dfrac{1}{2}SB=\sqrt{2}a;AN=\dfrac{1}{2}SD=\dfrac{a\sqrt{5}}{2}$ (đường trung tuyến trong tam giác vuông).
Ta có: $MN$ là đường trung bình của $\Delta SBD$ nên $MN=\dfrac{BD}{2}=\dfrac{a\sqrt{5}}{2}$.
Gọip là nửa chu vi tam giác $AMN$ ta có: $p=\dfrac{AM+AN+MN}{2}=\dfrac{\sqrt{2}a+\dfrac{a\sqrt{5}}{2}+\dfrac{a\sqrt{5}}{2}}{2}=\dfrac{\sqrt{2}+\sqrt{5}}{2}a$.
⇒ Diện tích tam giác $AMN$ là ${{S}_{AMN}}=\sqrt{p\left( p-AM \right)\left( p-AN \right)\left( p-MN \right)}=\dfrac{{{a}^{2}}\sqrt{6}}{4}$
Ta có: $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABD}}}=\dfrac{SM}{SB}.\dfrac{SN}{SD}=\dfrac{1}{4}$ $\Rightarrow {{V}_{S.AMN}}=\dfrac{1}{4}{{V}_{S.ABD}}=\dfrac{1}{8}{{V}_{S.ABCD}}$.
Mà ${{V}_{S.ABCD}}=\dfrac{1}{3}SA.{{S}_{ABCD}}=\dfrac{1}{3}.2a.2a.a=\dfrac{4{{a}^{3}}}{3}$ $\Rightarrow {{V}_{S.AMN}}=\dfrac{1}{8}.\dfrac{4{{a}^{3}}}{3}=\dfrac{{{a}^{3}}}{6}$.
Lại có ${{V}_{S.AMN}}=\dfrac{1}{3}d\left( S;\left( AMN \right) \right).{{S}_{AMN}}$, do đó $d\left( S;\left( AMN \right) \right)=\dfrac{3{{V}_{S.AMN}}}{{{S}_{AMN}}}=\dfrac{3.\dfrac{{{a}^{3}}}{6}}{\dfrac{{{a}^{2}}\sqrt{6}}{4}}=\dfrac{a\sqrt{6}}{3}$.
Vậy $d\left( S;\left( AMN \right) \right)=\dfrac{a\sqrt{6}}{3}$.
- Tính thể tích chóp $S.ABCD$, sử dụng tỉ lệ thể tích Simpson tính thể tích khối chóp ${{V}_{S.AMN}}$.
- Sử dụng công thức ${{V}_{S.AMN}}=\dfrac{1}{3}d\left( S;\left( AMN \right) \right).{{S}_{AMN}}\Rightarrow d\left( S;\left( AMN \right) \right)=\dfrac{3{{V}_{S.AMN}}}{{{S}_{AMN}}}$.
- Sử dụng định lí Pytago, định lí đường trung tuyến trong tam giác vuông, tính chất đường trung bình của tam giác tính độ dài các cạnh của tam giác $AMN$, sau đó sử dụng công thức Hê-rông tính diện tích tam giác $AMN$ : ${{S}_{AMN}}=\sqrt{p\left( p-AM \right)\left( p-AN \right)\left( p-MN \right)}$ với p là nửa chu vi $\Delta AMN$.
Giải chi tiết:
Áp dụng định lí Pytago trong các tam giác vuông $SAB,SAD,ABD$ ta có:
$SB=\sqrt{S{{A}^{2}}+A{{B}^{2}}}=\sqrt{4{{a}^{2}}+4{{a}^{2}}}=2\sqrt{2}a$
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=\sqrt{4{{a}^{2}}+{{a}^{2}}}=\sqrt{5}a$
$BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=\sqrt{4{{a}^{2}}+{{a}^{2}}}=\sqrt{5}a$
Khi đó ta có $AM=\dfrac{1}{2}SB=\sqrt{2}a;AN=\dfrac{1}{2}SD=\dfrac{a\sqrt{5}}{2}$ (đường trung tuyến trong tam giác vuông).
Ta có: $MN$ là đường trung bình của $\Delta SBD$ nên $MN=\dfrac{BD}{2}=\dfrac{a\sqrt{5}}{2}$.
Gọip là nửa chu vi tam giác $AMN$ ta có: $p=\dfrac{AM+AN+MN}{2}=\dfrac{\sqrt{2}a+\dfrac{a\sqrt{5}}{2}+\dfrac{a\sqrt{5}}{2}}{2}=\dfrac{\sqrt{2}+\sqrt{5}}{2}a$.
⇒ Diện tích tam giác $AMN$ là ${{S}_{AMN}}=\sqrt{p\left( p-AM \right)\left( p-AN \right)\left( p-MN \right)}=\dfrac{{{a}^{2}}\sqrt{6}}{4}$
Ta có: $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABD}}}=\dfrac{SM}{SB}.\dfrac{SN}{SD}=\dfrac{1}{4}$ $\Rightarrow {{V}_{S.AMN}}=\dfrac{1}{4}{{V}_{S.ABD}}=\dfrac{1}{8}{{V}_{S.ABCD}}$.
Mà ${{V}_{S.ABCD}}=\dfrac{1}{3}SA.{{S}_{ABCD}}=\dfrac{1}{3}.2a.2a.a=\dfrac{4{{a}^{3}}}{3}$ $\Rightarrow {{V}_{S.AMN}}=\dfrac{1}{8}.\dfrac{4{{a}^{3}}}{3}=\dfrac{{{a}^{3}}}{6}$.
Lại có ${{V}_{S.AMN}}=\dfrac{1}{3}d\left( S;\left( AMN \right) \right).{{S}_{AMN}}$, do đó $d\left( S;\left( AMN \right) \right)=\dfrac{3{{V}_{S.AMN}}}{{{S}_{AMN}}}=\dfrac{3.\dfrac{{{a}^{3}}}{6}}{\dfrac{{{a}^{2}}\sqrt{6}}{4}}=\dfrac{a\sqrt{6}}{3}$.
Vậy $d\left( S;\left( AMN \right) \right)=\dfrac{a\sqrt{6}}{3}$.
Đáp án A.