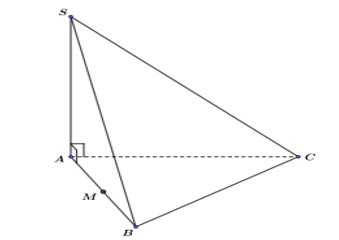
Cho hình chóp $S.ABC$, có đáy là tam giác đều cạnh $a$, cạnh bên...

Ta có hình vẽ sau
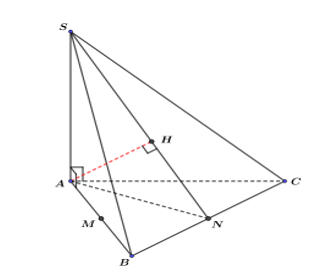Do $AB\cap \left( SBC \right)=B$, mà $M$ là trung điểm của cạnh $AB$ nên ta có:
$d=d\left( M;\left( SBC \right) \right)=\dfrac{1}{2}d\left( A;\left( SBC \right) \right)$.
Gọi $N$ là trung điểm của cạnh $BC$. Kẻ $AH\bot SN$ tại $H$ (1).
Ta có: $\left\{ \begin{aligned}
& BC\bot AN \\
& BC\bot SA \\
\end{aligned} \right.\Rightarrow BC\bot \left( SAN \right) $ $ \Rightarrow BC\bot AH$. (2)
Từ (1) và (2), ta có: $AH\bot \left( SBC \right)$ $\Rightarrow AH=d\left( A;\left( SBC \right) \right)$.
Trong tam giác vuông $ASN$ có $\left\{ \begin{aligned}
& AN=\dfrac{a\sqrt{3}}{2} \\
& SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=a\sqrt{2} \\
\end{aligned} \right.$ nên ta có:
$\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{N}^{2}}}+\dfrac{1}{S{{A}^{2}}}=\dfrac{11}{6{{a}^{2}}}$ $\Rightarrow AH=\dfrac{a\sqrt{66}}{11}$.
Như vậy $d=d\left( M;\left( SBC \right) \right)=\dfrac{1}{2}d\left( A;\left( SBC \right) \right)$ $=\dfrac{1}{2}AH=\dfrac{a\sqrt{66}}{22}$.