Google
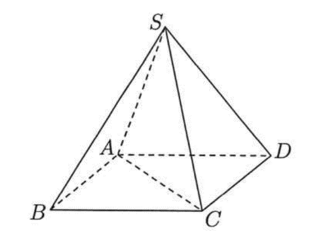
Câu hỏi: Cho hình chóp đều $S.ABCD$ có chiều cao $a, AC=2a$ (tham khảo hình bên). Tính khoảng cách từ điểm $B$ đến mặt phẳng $\left( SCD \right)$.
A. $\dfrac{\sqrt{3}}{3}a$.
B. $\sqrt{2}a$.
C. $\dfrac{2\sqrt{3}}{3}a$.
D. $\dfrac{\sqrt{2}}{2}a$.
- Gọi $O=AC\cap BD$, $H$ là trung điểm $CD$. Trong $\left( SOH \right)$, kẻ $OI\bot SH$.
Có $\left\{ \begin{aligned}
& CD\bot SO \\
& CD\bot SH \\
\end{aligned} \right.\Rightarrow CD\bot \left( SOH \right)\Rightarrow CD\bot OI$.
Mà $OI\bot SH$ nên $OI\bot \left( SCD \right)$ $\Rightarrow d\left( O,\left( SCD \right) \right)=OI$.
- Vì O là trung điểm BD nên $d\left( B,\left( SCD \right) \right)=d\left( O,\left( SCD \right) \right)=2OI=\dfrac{2SO.OH}{\sqrt{S{{O}^{2}}+O{{H}^{2}}}}$.
Có $AD=AC\sin 45{}^\circ =a\sqrt{2}$, $OH=a\dfrac{\sqrt{2}}{2}$ $\Rightarrow d\left( B,\left( SCD \right) \right)=\dfrac{2\sqrt{3}}{3}a$.
B. $\sqrt{2}a$.
C. $\dfrac{2\sqrt{3}}{3}a$.
D. $\dfrac{\sqrt{2}}{2}a$.
Có $\left\{ \begin{aligned}
& CD\bot SO \\
& CD\bot SH \\
\end{aligned} \right.\Rightarrow CD\bot \left( SOH \right)\Rightarrow CD\bot OI$.
Mà $OI\bot SH$ nên $OI\bot \left( SCD \right)$ $\Rightarrow d\left( O,\left( SCD \right) \right)=OI$.
- Vì O là trung điểm BD nên $d\left( B,\left( SCD \right) \right)=d\left( O,\left( SCD \right) \right)=2OI=\dfrac{2SO.OH}{\sqrt{S{{O}^{2}}+O{{H}^{2}}}}$.
Có $AD=AC\sin 45{}^\circ =a\sqrt{2}$, $OH=a\dfrac{\sqrt{2}}{2}$ $\Rightarrow d\left( B,\left( SCD \right) \right)=\dfrac{2\sqrt{3}}{3}a$.
Đáp án C.