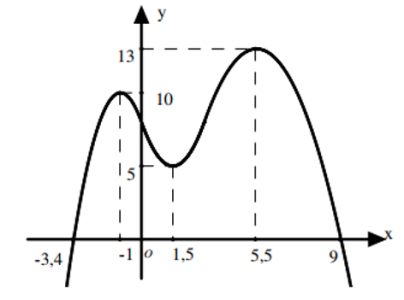
Câu hỏi: Cho hàm số $y=f(x)$ có đồ thị $y=f^{\prime}(x)$ như hình vẽ và $f^{\prime}(x)<0 \forall x \in(-\infty ;-3,4) \cup(9 ;+\infty)$. Đặt $g(x)=f(x)-m x+5$ với $m \in \mathbb{N}$. Có bao nhiêu giá trị của $m$ để hàm số $y=g(x)$ có đúng hai điểm cực trị?
A. 8 .
B. 11 .
C. 9 .
D. 10 .
A. 8 .
B. 11 .
C. 9 .
D. 10 .
Ta có $g^{\prime}(x)=f^{\prime}(x)-m$. Suy ra: $g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=m$.
Do đó: Số nghiệm của phương trình $g^{\prime}(x)=0$ tương đương với số giao điểm của đồ thị hàm số $f^{\prime}(x)$ và đường thẳng $y=m$.
Nhận xét: Hàm số $y=g(x)$ có đúng hai điểm cực trị khi và chỉ khi phương trình $g^{\prime}(x)=0$ có số nghiệm lớn hơn bằng 2 , trong đó có đúng 2 nghiệm đơn.
Dựa vào đồ thị và các lập luận trên, suy ra $\left[\begin{array}{l}m \leq 5 \\ 10 \leq m<13\end{array}\right.$, mà $m \in \mathbb{N}$ nên $m \in\{0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 10 ; 11 ; 12\}$.
Vậy có 9 giá trị $m$ thỏa mãn.
Do đó: Số nghiệm của phương trình $g^{\prime}(x)=0$ tương đương với số giao điểm của đồ thị hàm số $f^{\prime}(x)$ và đường thẳng $y=m$.
Nhận xét: Hàm số $y=g(x)$ có đúng hai điểm cực trị khi và chỉ khi phương trình $g^{\prime}(x)=0$ có số nghiệm lớn hơn bằng 2 , trong đó có đúng 2 nghiệm đơn.
Dựa vào đồ thị và các lập luận trên, suy ra $\left[\begin{array}{l}m \leq 5 \\ 10 \leq m<13\end{array}\right.$, mà $m \in \mathbb{N}$ nên $m \in\{0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 10 ; 11 ; 12\}$.
Vậy có 9 giá trị $m$ thỏa mãn.
Đáp án C.