Google
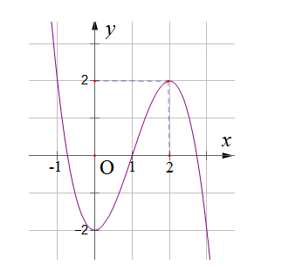
Câu hỏi: Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$. Biết rằng hàm số $y=f^{\prime}(x)$ có đồ thị như hình vẽ dưới đây:
Đặt $g(x)=f(x)+x$. Hỏi hàm số có bao nhiêu điểm cực đại và bao nhiêu điểm cực tiểu?
A. Hàm số không có điểm cực đại và một điểm cực tiểu.
B. Hàm số có một điểm cực đại và một điểm cực tiểu.
C. Hàm số có hai điểm cực đại và một điểm cực tiểu.
D. Hàm số có một điểm cực đại và một điểm cực tiểu.
A. Hàm số không có điểm cực đại và một điểm cực tiểu.
B. Hàm số có một điểm cực đại và một điểm cực tiểu.
C. Hàm số có hai điểm cực đại và một điểm cực tiểu.
D. Hàm số có một điểm cực đại và một điểm cực tiểu.
Hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ nên $g(x)=f(x)+x$ cũng có đạo hàm trên $\mathbb{R}$ và $g^{\prime}(x)=f^{\prime}(x)+$ $1 ; g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=-1$
Dựa vào đồ thị $f^{\prime}(x)$ ta có $\forall x \in[1 ; 4]$ có ba nghiệm phân biệt $x_1, x_2$ và $x_3$ với $x_1<x_2<x_3$. Bảng biến thiên của $g(x)$ :
Hàm số có hai điểm cực đại và một điểm cực tiểu.
Dựa vào đồ thị $f^{\prime}(x)$ ta có $\forall x \in[1 ; 4]$ có ba nghiệm phân biệt $x_1, x_2$ và $x_3$ với $x_1<x_2<x_3$. Bảng biến thiên của $g(x)$ :
Đáp án C.