Google
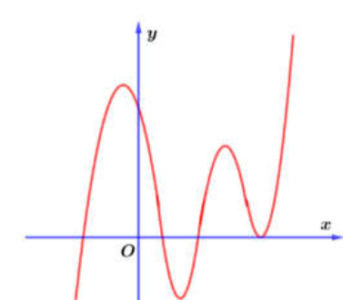
Câu hỏi: Cho hàm số $y=f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có đồ thị của đạo hàm $y={f}'\left( x \right)$ như hình vẽ bên dưới. Số điểm cực tiểu của hàm số $y=f\left( x \right)$ là:
A. $3$.
B. $1$.
C. $4$.
D. $2$.
B. $1$.
C. $4$.
D. $2$.
+ Giả sử đồ thị hàm số $y={f}'\left( x \right)$ cắt $Ox$ tại $4$ điểm theo thứ tự $a<b<c<d$, khi đó ${f}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=a \\
& x=b \\
& x=c \\
& x=d \\
\end{aligned} \right.$.
+ Ta có BBT của hàm số $y=f\left( x \right)$ như sau:
+Nhìn BBT, ta thấy hàm số $y=f\left( x \right)$ có hai điểm cực tiểu.
& x=a \\
& x=b \\
& x=c \\
& x=d \\
\end{aligned} \right.$.
+ Ta có BBT của hàm số $y=f\left( x \right)$ như sau:
Đáp án D.