Google
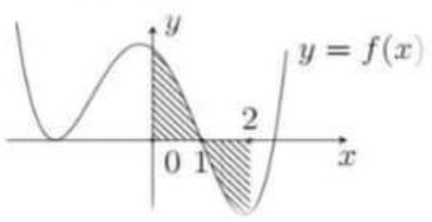
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị $\left( C \right)$ là đường cong như hình bên.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $\left( C \right)$, trục hoành và hai đường thẳng $x=0;$ $x=2$ là
A. $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}-\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
B. $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}+\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
C. $\left| \int\limits_{0}^{2}{f\left( x \right)\text{d}x} \right|$.
D. $\int\limits_{0}^{2}{f\left( x \right)\text{d}x}$.
A. $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}-\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
B. $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}+\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
C. $\left| \int\limits_{0}^{2}{f\left( x \right)\text{d}x} \right|$.
D. $\int\limits_{0}^{2}{f\left( x \right)\text{d}x}$.
Dựa vào đồ thị hàm số ta có diện tích hình phẳng cần tính là $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}-\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
Đáp án A.