Google
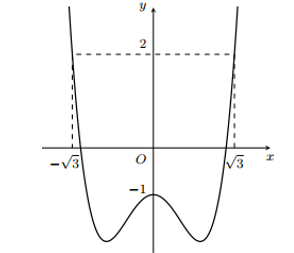
Câu hỏi: Cho hàm số $y=f\left( x \right)$. Đồ thị hàm số đạo hàm $y={f}'\left( x \right)$ như hình vẽ bên. Đặt $h\left( x \right)=3f\left( x \right)-{{x}^{3}}+3x$. Tìm mệnh đề đúng trong các mệnh đề sau?
A. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( \sqrt{3} \right)$.
B. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( 0 \right)$.
C. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( 1 \right)$.
D. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( -\sqrt{3} \right)$.
B. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( 0 \right)$.
C. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( 1 \right)$.
D. $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( -\sqrt{3} \right)$.
Ta có ${h}'\left( x \right)=3\left[ {f}'\left( x \right)-{{x}^{2}}+1 \right]$ nên ${h}'\left( x \right)=3\left[ {f}'\left( x \right)-{{x}^{2}}+1 \right]=0\Leftrightarrow {f}'\left( x \right)={{x}^{2}}-1$.
Vẽ đồ thị hai hàm số
Suy ra ${f}'\left( x \right)={{x}^{2}}-1\Leftrightarrow \left[ \begin{aligned}
& x=\pm \sqrt{3} \\
& x=0. \\
\end{aligned} \right.$
Lập bảng biến thiên
Từ bảng biến thiên ta có $\underset{\left[ -\sqrt{3};\sqrt{3} \right]}{\mathop{\max }} h\left( x \right)=3f\left( -\sqrt{3} \right)$.
Vẽ đồ thị hai hàm số
& x=\pm \sqrt{3} \\
& x=0. \\
\end{aligned} \right.$
Lập bảng biến thiên
Đáp án D.