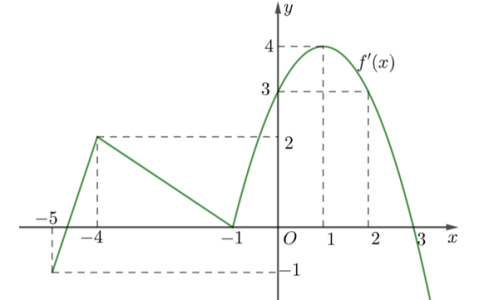
Cho hàm số $y=f\left( x \right)$. Đồ thị của hàm số $y={f}'\left(...

Kí hiệu các điểm như hình vẽ.
Đường thẳng $AB$ đi qua hai điểm $A\left( -5;-1 \right)$ và $B\left( -4;2 \right)$ nên có phương trình $y=3x+14$.
Đường thẳng $BC$ đi qua hai điểm $B\left( -4;2 \right)$ và $C\left( -1;0 \right)$ nên có phương trình $y=-\dfrac{2}{3}x-\dfrac{2}{3}$.
Parabol $y=a{{x}^{2}}+bx+c$ đi qua các điểm $C\left( -1;0 \right)$, $D\left( 0;3 \right)$, $E\left( 3;0 \right)$ nên ta có hệ phương trình
$\left\{ \begin{aligned}
& a-b+c=0 \\
& c=3 \\
& 9a+3b+c=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=-1 \\
& b=2 \\
& c=3 \\
\end{aligned} \right.$.
Do đó ${f}'\left( x \right)=\left\{ \begin{aligned}
& 3x+14\text{ khi }x\in \left( -5;-4 \right) \\
& -\dfrac{2}{3}x-\dfrac{2}{3}\text{ khi }x\in \left( -4;-1 \right) \\
& -{{x}^{2}}+2x+3\text{ khi }x\in \left( -1;3 \right) \\
\end{aligned} \right.$.
Ta có $f\left( 0 \right)-f\left( -5 \right)=\int\limits_{-5}^{0}{{f}'\left( x \right)\text{d}x}=\int\limits_{-5}^{-4}{\left( 3x+14 \right)\text{d}x}+\int\limits_{-4}^{-1}{\left( -\dfrac{2}{3}x-\dfrac{2}{3} \right)\text{d}x}+\int\limits_{-1}^{0}{\left( -{{x}^{2}}+2x+3 \right)\text{d}x}=\dfrac{31}{6}$.
Vì $f\left( 0 \right)=0$ nên $f\left( -5 \right)=-\dfrac{31}{6}$.
Lại có $f\left( 2 \right)-f\left( 0 \right)=\int\limits_{0}^{2}{{f}'\left( x \right)\text{d}x}=\int\limits_{0}^{2}{\left( -{{x}^{2}}+2x+3 \right)\text{d}x}=\dfrac{22}{3}$.
Vì $f\left( 0 \right)=0$ nên $f\left( 2 \right)=\dfrac{22}{3}$.
Vậy $2f\left( -5 \right)+3f\left( 2 \right)=\dfrac{35}{3}$.