Google
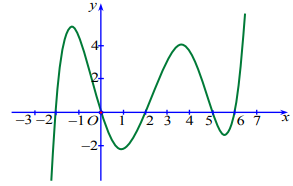
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc đoạn $\left[ -2;6 \right]$ của phương trình $f\left( x \right)=f\left( 0 \right)$
A. $4$.
B. $3$.
C. $5$.
D. $2$.
A. $4$.
B. $3$.
C. $5$.
D. $2$.
Dựa vào đồ thị hàm số $y={f}'\left( x \right)$
Ta có $-\int\limits_{0}^{2}{{f}'\left( x \right)dx}<\int\limits_{2}^{5}{{f}'\left( x \right)dx}$ hay $-\left( f\left( 2 \right)-f\left( 0 \right) \right)<f\left( 5 \right)-f\left( 2 \right)\Leftrightarrow f\left( 0 \right)<f\left( 5 \right)$
Dựa vào đồ thị ta có bảng biến thiên sau
Dựa bảng biến thiên suy ra phương trình $f\left( x \right)=f\left( 0 \right)$ có 3 nghiệm phân biệt.
Ta có $-\int\limits_{0}^{2}{{f}'\left( x \right)dx}<\int\limits_{2}^{5}{{f}'\left( x \right)dx}$ hay $-\left( f\left( 2 \right)-f\left( 0 \right) \right)<f\left( 5 \right)-f\left( 2 \right)\Leftrightarrow f\left( 0 \right)<f\left( 5 \right)$
Dựa vào đồ thị ta có bảng biến thiên sau
Dựa bảng biến thiên suy ra phương trình $f\left( x \right)=f\left( 0 \right)$ có 3 nghiệm phân biệt.
Đáp án B.