Google
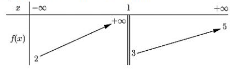
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\dfrac{3}{2f\left( x \right)-8}$ là
A. $3$.
B. $2$.
C. $4$.
D. $5$.
A. $3$.
B. $2$.
C. $4$.
D. $5$.
Ta có:
+ $\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=5\Rightarrow \underset{x\to +\infty }{\mathop{\lim }} \dfrac{3}{2f\left( x \right)-8}=\dfrac{3}{2}$,
+ $\underset{x\to \infty }{\mathop{\lim }} f\left( x \right)=2\Rightarrow \underset{x\to +\infty }{\mathop{\lim }} \dfrac{3}{2f\left( x \right)-8}=-\dfrac{3}{4}$,
Đồ thị có 2 TCN là hai đường thẳng: $y=\dfrac{3}{2}; y=-\dfrac{3}{4}$.
- Xét phương trình $f\left( x \right)=4$ có 2 nghiệm là $x=\alpha ; x=\beta $, khi đó$$
+ $\underset{x\to \alpha }{\mathop{\lim }} \frac{3}{2f\left( x \right)-8}=-\infty \left( +\infty \right);\underset{ x\to \beta }{\mathop{ \lim }} \frac{3}{2f\left( x \right)-8}=+\infty \left( -\infty \right)$
Đồ thị có 2 TCĐ là hai đường thẳng $x=\alpha ; x=\beta $.
Vậy đồ thị có 4 đường TC.
+ $\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=5\Rightarrow \underset{x\to +\infty }{\mathop{\lim }} \dfrac{3}{2f\left( x \right)-8}=\dfrac{3}{2}$,
+ $\underset{x\to \infty }{\mathop{\lim }} f\left( x \right)=2\Rightarrow \underset{x\to +\infty }{\mathop{\lim }} \dfrac{3}{2f\left( x \right)-8}=-\dfrac{3}{4}$,
Đồ thị có 2 TCN là hai đường thẳng: $y=\dfrac{3}{2}; y=-\dfrac{3}{4}$.
- Xét phương trình $f\left( x \right)=4$ có 2 nghiệm là $x=\alpha ; x=\beta $, khi đó$$
+ $\underset{x\to \alpha }{\mathop{\lim }} \frac{3}{2f\left( x \right)-8}=-\infty \left( +\infty \right);\underset{ x\to \beta }{\mathop{ \lim }} \frac{3}{2f\left( x \right)-8}=+\infty \left( -\infty \right)$
Đồ thị có 2 TCĐ là hai đường thẳng $x=\alpha ; x=\beta $.
Vậy đồ thị có 4 đường TC.
Đáp án C.