Google
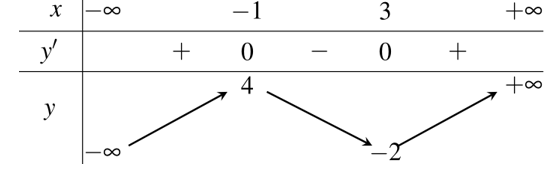
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:
Số đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{2023}{f\left( x \right)}$ là
A. $0.$
B. $2.$
C. $3.$
D. $1.$
A. $0.$
B. $2.$
C. $3.$
D. $1.$
Từ bảng biến thiên ta thấy $f\left( x \right)=0$ có 3 nghiệm ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ phân biệt.
Do vậy $\underset{x\to {{x}_{1}}}{\mathop{\lim }} y=\pm \infty ;\underset{x\to {{x}_{2}}}{\mathop{\lim }} y=\pm \infty ;\underset{x\to {{x}_{3}}}{\mathop{\lim }} y=\pm \infty $ nên đồ thị hàm số $y=\dfrac{2023}{f\left( x \right)}$ có 3 đường tiệm cận đứng.
Do vậy $\underset{x\to {{x}_{1}}}{\mathop{\lim }} y=\pm \infty ;\underset{x\to {{x}_{2}}}{\mathop{\lim }} y=\pm \infty ;\underset{x\to {{x}_{3}}}{\mathop{\lim }} y=\pm \infty $ nên đồ thị hàm số $y=\dfrac{2023}{f\left( x \right)}$ có 3 đường tiệm cận đứng.
Đáp án B.