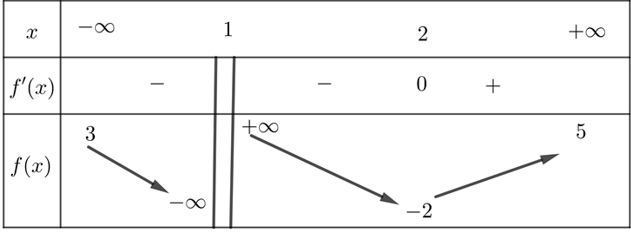
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. $3$.
B. $1$.
C. $2$.
D. $4$.
A. $3$.
B. $1$.
C. $2$.
D. $4$.
Ta có:
$\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=5; \underset{x\to -\infty }{\mathop{\lim }} f\left( x \right)=3$ $\Rightarrow $ đồ thị hàm số có hai đường tiệm cận ngang là $y=3$ và $y=5$.
$\underset{x\to {{1}^{-}}}{\mathop{\lim }} f\left( x \right)=-\infty ; \underset{x\to {{1}^{+}}}{\mathop{\lim }} f\left( x \right)=+\infty $ $\Rightarrow $ đồ thị hàm số có đường tiệm cận đứng là $x=1$.
Vậy đồ thị hàm số có 3 đường tiệm cận.
$\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=5; \underset{x\to -\infty }{\mathop{\lim }} f\left( x \right)=3$ $\Rightarrow $ đồ thị hàm số có hai đường tiệm cận ngang là $y=3$ và $y=5$.
$\underset{x\to {{1}^{-}}}{\mathop{\lim }} f\left( x \right)=-\infty ; \underset{x\to {{1}^{+}}}{\mathop{\lim }} f\left( x \right)=+\infty $ $\Rightarrow $ đồ thị hàm số có đường tiệm cận đứng là $x=1$.
Vậy đồ thị hàm số có 3 đường tiệm cận.
Đáp án A.