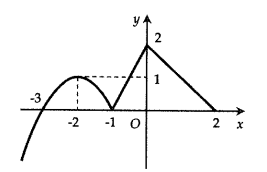
Câu hỏi: Cho hàm số $f(x)$. Đồ thị của hàm số $y={f}'(x)$ trên $\left[ -3;2 \right]$ như hình vẽ (phần cong của đồ thị là một phần của parabol $y=a{{x}^{2}}+bx+c$ ).
Biết $f(-3)=0$, giá trị của $f(-1)+f(1)$ bằng
A. $\dfrac{23}{6}$
B. $\dfrac{31}{6}$
C. $\dfrac{35}{3}$
D. $\dfrac{9}{2}$
Biết $f(-3)=0$, giá trị của $f(-1)+f(1)$ bằng
A. $\dfrac{23}{6}$
B. $\dfrac{31}{6}$
C. $\dfrac{35}{3}$
D. $\dfrac{9}{2}$
Cách 1: Giải bằng phương pháp tự luận dùng nguyên hàm
Ta xác định biểu thức của hàm số $y={f}'(x)$. Từ hình vẽ ta thấy trên $\left[ -3;2 \right]$ đồ thị gồm 3 nhánh:
- Nhánh parabol $y={{a}_{1}}{{x}^{2}}+{{b}_{1}}x+{{c}_{1}}$ xác định trên $\left[ -3;-1 \right]$ đi qua 3 điểm $(-3;0),(-2;1)$ và $(-1;0)$.
- Nhánh đường thẳng $y={{a}_{2}}x+{{b}_{2}}$ xác định trên $\left[ -1;0 \right]$ đi qua 2 điểm $(-1;0)$ và $(0;2)$.
- Nhánh đường thẳng $y={{a}_{3}}x+{{b}_{3}}$ xác định trên $\left[ 0;2 \right]$ đi qua 2 điểm $(0;2)$ và $(2;0)$.
Từ đây, giải các hệ phương trình tương ứng ta suy ra biểu thức của ${f}'(x)$ là:
${f}'(x)=\left\{ \begin{aligned}
& -{{x}^{2}}-4\text{x}-3\text{ khi }-3\le x\le -1 \\
& 2\text{x}+2\text{ khi }-1\le x\le 0 \\
& -x+2\text{ khi }0\le x\le 2 \\
\end{aligned} \right.$.
$f(x)$ là một nguyên hàm của ${f}'(x)$, do đó biểu thức của $f(x)$ có dạng:
$f(x)=\left\{ \begin{aligned}
& -\dfrac{{{x}^{3}}}{3}-2{{\text{x}}^{2}}-3\text{x}+{{C}_{1}}\text{ khi }-3\le x\le -1 \\
& {{x}^{2}}+2x+{{C}_{2}}\text{ khi }-1\le \text{x}\le 0 \\
& -\dfrac{{{x}^{2}}}{2}+2\text{x}+{{C}_{3}}\text{ khi }0\le x\le 2 \\
\end{aligned} \right.$.
Vì $f(-3)=0$ nên ta có: $-\dfrac{{{(-3)}^{3}}}{3}-2{{(-3)}^{2}}-3(-3)+{{C}_{1}}=0\Leftrightarrow {{C}_{1}}=0$.
Do $f$ liên tục tại $x=-1$ nên ta có: $\underset{x\to -{{1}^{-}}}{\mathop{\lim }} f(x)=\underset{x\to -{{1}^{+}}}{\mathop{\lim }} f(x)$, suy ra:
$-\dfrac{{{(-1)}^{3}}}{3}-2{{(-1)}^{2}}-3(-1)={{(-1)}^{2}}+2(-1)+{{C}_{2}}\Leftrightarrow {{C}_{2}}=\dfrac{7}{3}$.
Tương tự, $f$ liên tục tại $x=0$ nên ta có: ${{0}^{2}}+2.0+\dfrac{7}{3}=-\dfrac{{{0}^{2}}}{2}+2.0+{{C}_{3}}\Leftrightarrow {{C}_{3}}=\dfrac{7}{3}$.
Vậy $f(-1)+f(1)=\left[ {{(-1)}^{2}}+2(-1)+\dfrac{7}{3} \right]+\left[ -\dfrac{{{1}^{2}}}{2}+2.1+\dfrac{7}{3} \right]=\dfrac{31}{6}$.
Cách 2: Giải nhanh bằng phương pháp đánh giá diện tích trên đồ thị

Diện tích hình phẳng giới hạn bởi một parabol và một đường thẳng có phương song song với trục Ox được cho bởi công thức: $S=\dfrac{2}{3}$ đáy $\times $ cao (1)
Áp dụng công thức này ta giải nhanh bài toán này như sau:

Nhánh parabol $y=a{{x}^{2}}+bx+c$ qua 3 điểm $(-3;0),(-2;1)$ và $(-1;0)$ nên ta tính ra được hệ số $a=-1$.
Ta có:
$f(-1)+f(1)=\left[ f(-1)-f(-3) \right]+\left[ f(1)-f(-3) \right]={{S}_{1}}+({{S}_{1}}+{{S}_{2}}+{{S}_{3}})$.
Với: ${{S}_{1}}=\dfrac{2}{3}.2.1=\dfrac{4}{3},{{\text{S}}_{2}}=\dfrac{1}{2}.1.2=1,{{\text{S}}_{3}}=\dfrac{1}{2}(1+2).1=\dfrac{3}{2}$.
Suy ra: $f(-1)+f(1)=\dfrac{31}{6}$.
Ta xác định biểu thức của hàm số $y={f}'(x)$. Từ hình vẽ ta thấy trên $\left[ -3;2 \right]$ đồ thị gồm 3 nhánh:
- Nhánh parabol $y={{a}_{1}}{{x}^{2}}+{{b}_{1}}x+{{c}_{1}}$ xác định trên $\left[ -3;-1 \right]$ đi qua 3 điểm $(-3;0),(-2;1)$ và $(-1;0)$.
- Nhánh đường thẳng $y={{a}_{2}}x+{{b}_{2}}$ xác định trên $\left[ -1;0 \right]$ đi qua 2 điểm $(-1;0)$ và $(0;2)$.
- Nhánh đường thẳng $y={{a}_{3}}x+{{b}_{3}}$ xác định trên $\left[ 0;2 \right]$ đi qua 2 điểm $(0;2)$ và $(2;0)$.
Từ đây, giải các hệ phương trình tương ứng ta suy ra biểu thức của ${f}'(x)$ là:
${f}'(x)=\left\{ \begin{aligned}
& -{{x}^{2}}-4\text{x}-3\text{ khi }-3\le x\le -1 \\
& 2\text{x}+2\text{ khi }-1\le x\le 0 \\
& -x+2\text{ khi }0\le x\le 2 \\
\end{aligned} \right.$.
$f(x)$ là một nguyên hàm của ${f}'(x)$, do đó biểu thức của $f(x)$ có dạng:
$f(x)=\left\{ \begin{aligned}
& -\dfrac{{{x}^{3}}}{3}-2{{\text{x}}^{2}}-3\text{x}+{{C}_{1}}\text{ khi }-3\le x\le -1 \\
& {{x}^{2}}+2x+{{C}_{2}}\text{ khi }-1\le \text{x}\le 0 \\
& -\dfrac{{{x}^{2}}}{2}+2\text{x}+{{C}_{3}}\text{ khi }0\le x\le 2 \\
\end{aligned} \right.$.
Vì $f(-3)=0$ nên ta có: $-\dfrac{{{(-3)}^{3}}}{3}-2{{(-3)}^{2}}-3(-3)+{{C}_{1}}=0\Leftrightarrow {{C}_{1}}=0$.
Do $f$ liên tục tại $x=-1$ nên ta có: $\underset{x\to -{{1}^{-}}}{\mathop{\lim }} f(x)=\underset{x\to -{{1}^{+}}}{\mathop{\lim }} f(x)$, suy ra:
$-\dfrac{{{(-1)}^{3}}}{3}-2{{(-1)}^{2}}-3(-1)={{(-1)}^{2}}+2(-1)+{{C}_{2}}\Leftrightarrow {{C}_{2}}=\dfrac{7}{3}$.
Tương tự, $f$ liên tục tại $x=0$ nên ta có: ${{0}^{2}}+2.0+\dfrac{7}{3}=-\dfrac{{{0}^{2}}}{2}+2.0+{{C}_{3}}\Leftrightarrow {{C}_{3}}=\dfrac{7}{3}$.
Vậy $f(-1)+f(1)=\left[ {{(-1)}^{2}}+2(-1)+\dfrac{7}{3} \right]+\left[ -\dfrac{{{1}^{2}}}{2}+2.1+\dfrac{7}{3} \right]=\dfrac{31}{6}$.
Cách 2: Giải nhanh bằng phương pháp đánh giá diện tích trên đồ thị
Diện tích hình phẳng giới hạn bởi một parabol và một đường thẳng có phương song song với trục Ox được cho bởi công thức: $S=\dfrac{2}{3}$ đáy $\times $ cao (1)
Áp dụng công thức này ta giải nhanh bài toán này như sau:
Nhánh parabol $y=a{{x}^{2}}+bx+c$ qua 3 điểm $(-3;0),(-2;1)$ và $(-1;0)$ nên ta tính ra được hệ số $a=-1$.
Ta có:
$f(-1)+f(1)=\left[ f(-1)-f(-3) \right]+\left[ f(1)-f(-3) \right]={{S}_{1}}+({{S}_{1}}+{{S}_{2}}+{{S}_{3}})$.
Với: ${{S}_{1}}=\dfrac{2}{3}.2.1=\dfrac{4}{3},{{\text{S}}_{2}}=\dfrac{1}{2}.1.2=1,{{\text{S}}_{3}}=\dfrac{1}{2}(1+2).1=\dfrac{3}{2}$.
Suy ra: $f(-1)+f(1)=\dfrac{31}{6}$.
Đáp án B.