Google
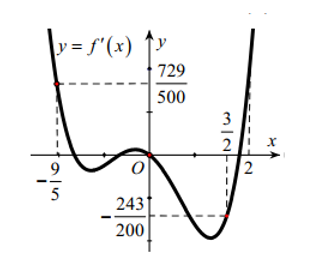
Câu hỏi: Cho hàm số $f(x)$ có $f''(0)=-\dfrac{81}{100}$ và đồ thị của hàm số $y=f'(x)$ như hình bên dưới
Hỏi hàm số $y=\left| f(x)+\dfrac{81}{200}{{x}^{2}}-m \right|$, ( $m$ là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng $\left( -\dfrac{9}{5};2 \right]?$
A. $4$.
B. $6$.
C. $3$.
D. $5$.
Xét hàm số $g(x)=f(x)+\dfrac{81}{200}{{x}^{2}}-m$
Ta có $g'(x)=f'(x)+\dfrac{81}{100}x$. Từ đồ thị của hàm số $y=f'(x)$ và đường thẳng $y=-\dfrac{81}{100}x$ ta có
$g'(x)=0\Leftrightarrow f'(x)=-\dfrac{81}{100}x\Leftrightarrow $ $\left[ \begin{aligned}
& x=-\dfrac{9}{5} \\
& x=0 \\
& x=\dfrac{3}{2} \\
\end{aligned} \right.$
Đường thẳng $y=-\dfrac{81}{100}x$ có hệ số góc bẳng $-\dfrac{81}{100}$
Mà $f''(0)=-\dfrac{81}{100}$ nên đường thẳng $y=-\dfrac{81}{100}x$ tiếp xúc với đồ thị của hàm số $y=f'(x)$
Ta có bảng xét dấu
Dựa vào BBT, suy ra hàm số $y=\left| g(x) \right|$ có nhiều nhất $3$ điểm cực trị trên nửa khoảng $\left( -\dfrac{9}{5};2 \right].$
A. $4$.
B. $6$.
C. $3$.
D. $5$.
Ta có $g'(x)=f'(x)+\dfrac{81}{100}x$. Từ đồ thị của hàm số $y=f'(x)$ và đường thẳng $y=-\dfrac{81}{100}x$ ta có
$g'(x)=0\Leftrightarrow f'(x)=-\dfrac{81}{100}x\Leftrightarrow $ $\left[ \begin{aligned}
& x=-\dfrac{9}{5} \\
& x=0 \\
& x=\dfrac{3}{2} \\
\end{aligned} \right.$
Đường thẳng $y=-\dfrac{81}{100}x$ có hệ số góc bẳng $-\dfrac{81}{100}$
Mà $f''(0)=-\dfrac{81}{100}$ nên đường thẳng $y=-\dfrac{81}{100}x$ tiếp xúc với đồ thị của hàm số $y=f'(x)$
Ta có bảng xét dấu
Đáp án C.