Google
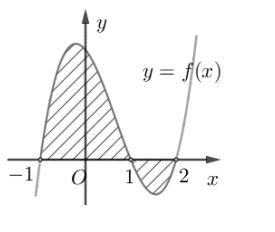
Câu hỏi: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=f\left( x \right), y=0, x=-1, x=2$. Mệnh đề nào dưới đây đúng?
A. $S=\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x + \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
B. $S=\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x - \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
C. $S=-\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x - \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
D. $S=-\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x + \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
B. $S=\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x - \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
C. $S=-\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x - \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
D. $S=-\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x + \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
Ta có $S=\int\limits_{-1}^{2}{\left| f\left( x \right) \right|}\text{d}x =\int\limits_{-1}^{1}{\left| f\left( x \right) \right|}\text{d}x + \int\limits_{1}^{2}{\left| f\left( x \right) \right|}\text{d}x =\int\limits_{-1}^{1}{f\left( x \right)}\text{d}x - \int\limits_{1}^{2}{f\left( x \right)}\text{d}x$.
Đáp án A.