Google
Câu hỏi: Cho hàm số $f\left( x \right)={{e}^{2022x}}-{{e}^{-2022x}}+{{\ln }^{2023}}\left( x+\sqrt{{{x}^{2}}+1} \right)$. Trên khoảng $\left( -25;25 \right)$ có tất cả bao nhiêu giá trị nguyên của tham số $m$ sao cho phương trình $f\left( {{e}^{x+m}}+m \right)+f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=0$ có đúng ba nghiệm phân biệt?
A. $25$.
B. $26$.
C. $24$.
D. $48$.
A. $25$.
B. $26$.
C. $24$.
D. $48$.
Hàm số $f\left( x \right)$ có tập xác định $D=\mathbb{R}$ nên $\forall x\in D\Rightarrow -x\in D$.
Ta có $f\left( -x \right)={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\left( -x+\sqrt{{{\left( -x \right)}^{2}}+1} \right)={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\left( -x+\sqrt{{{x}^{2}}+1} \right)$
$={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\dfrac{1}{\sqrt{{{x}^{2}}+1}+x}={{e}^{-2022x}}-{{e}^{2022x}}-{{\ln }^{2023}}\left( x+\sqrt{{{x}^{2}}+1} \right)=-f\left( x \right)$.
Do đó $f\left( x \right)$ là hàm số lẻ. Suy ra $f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=-f\left( \ln {{x}^{2}}+{{x}^{2}}-x \right)$.
Mặt khác ta có ${f}'\left( x \right)=2022{{e}^{2022x}}+2022{{e}^{-2022x}}+2023.{{\ln }^{2022}}\left( x+\sqrt{{{x}^{2}}+1} \right).\dfrac{1}{\sqrt{{{x}^{2}}+1}}>0, \forall x\in \mathbb{R}$, suy ra hàm số $f\left( x \right)$ đồng biến trên $\mathbb{R}$.
Khi đó phương trình $f\left( {{e}^{x+m}}+m \right)+f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=0$ $\Leftrightarrow f\left( {{e}^{x+m}}+m \right)=f\left( \ln {{x}^{2}}+{{x}^{2}}-x \right)$
${{e}^{x+m}}+m=\ln {{x}^{2}}+{{x}^{2}}-x\Leftrightarrow {{e}^{x+m}}+x+m=\ln {{x}^{2}}+{{x}^{2}}\Leftrightarrow {{e}^{x+m}}+x+m={{e}^{\ln {{x}^{2}}}}+\ln {{x}^{2}} \left( * \right)$.
Xét hàm số $g\left( t \right)={{e}^{t}}+t\Rightarrow {g}'\left( t \right)={{e}^{t}}+1>0, \forall t\in \mathbb{R}$.
Suy ra hàm số $g\left( t \right)$ đồng biến trên $\mathbb{R}$.
$\left( * \right)$ có dạng $g\left( x+m \right)=g\left( \ln {{x}^{2}} \right)$. Do đó $x+m=\ln {{x}^{2}}\Leftrightarrow m=\ln {{x}^{2}}-x$.
Xét hàm số $h\left( x \right)=\ln {{x}^{2}}-x\Rightarrow {h}'\left( x \right)=\dfrac{2}{x}-1\Rightarrow {h}'\left( x \right)=0\Leftrightarrow x=2$.
BBT:
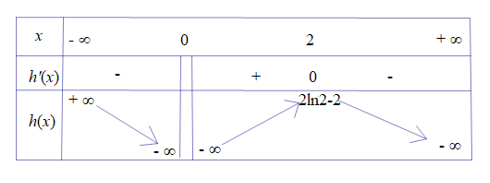Phương trình $f\left( {{e}^{x+m}}+m \right)+f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=0$ có ba nghiệm phân biệt $\Leftrightarrow m<2\ln 2-2$.
Mà $m\in \left( -25;25 \right), m\in \mathbb{Z}\Rightarrow m\in \left\{ -24; -23; ... ;-1 \right\}$.
Vậy có 24 giá trị của tham số $m$ thỏa mãn bài toán đã cho.
Ta có $f\left( -x \right)={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\left( -x+\sqrt{{{\left( -x \right)}^{2}}+1} \right)={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\left( -x+\sqrt{{{x}^{2}}+1} \right)$
$={{e}^{-2022x}}-{{e}^{2022x}}+{{\ln }^{2023}}\dfrac{1}{\sqrt{{{x}^{2}}+1}+x}={{e}^{-2022x}}-{{e}^{2022x}}-{{\ln }^{2023}}\left( x+\sqrt{{{x}^{2}}+1} \right)=-f\left( x \right)$.
Do đó $f\left( x \right)$ là hàm số lẻ. Suy ra $f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=-f\left( \ln {{x}^{2}}+{{x}^{2}}-x \right)$.
Mặt khác ta có ${f}'\left( x \right)=2022{{e}^{2022x}}+2022{{e}^{-2022x}}+2023.{{\ln }^{2022}}\left( x+\sqrt{{{x}^{2}}+1} \right).\dfrac{1}{\sqrt{{{x}^{2}}+1}}>0, \forall x\in \mathbb{R}$, suy ra hàm số $f\left( x \right)$ đồng biến trên $\mathbb{R}$.
Khi đó phương trình $f\left( {{e}^{x+m}}+m \right)+f\left( x-{{x}^{2}}-\ln {{x}^{2}} \right)=0$ $\Leftrightarrow f\left( {{e}^{x+m}}+m \right)=f\left( \ln {{x}^{2}}+{{x}^{2}}-x \right)$
${{e}^{x+m}}+m=\ln {{x}^{2}}+{{x}^{2}}-x\Leftrightarrow {{e}^{x+m}}+x+m=\ln {{x}^{2}}+{{x}^{2}}\Leftrightarrow {{e}^{x+m}}+x+m={{e}^{\ln {{x}^{2}}}}+\ln {{x}^{2}} \left( * \right)$.
Xét hàm số $g\left( t \right)={{e}^{t}}+t\Rightarrow {g}'\left( t \right)={{e}^{t}}+1>0, \forall t\in \mathbb{R}$.
Suy ra hàm số $g\left( t \right)$ đồng biến trên $\mathbb{R}$.
$\left( * \right)$ có dạng $g\left( x+m \right)=g\left( \ln {{x}^{2}} \right)$. Do đó $x+m=\ln {{x}^{2}}\Leftrightarrow m=\ln {{x}^{2}}-x$.
Xét hàm số $h\left( x \right)=\ln {{x}^{2}}-x\Rightarrow {h}'\left( x \right)=\dfrac{2}{x}-1\Rightarrow {h}'\left( x \right)=0\Leftrightarrow x=2$.
BBT:
Mà $m\in \left( -25;25 \right), m\in \mathbb{Z}\Rightarrow m\in \left\{ -24; -23; ... ;-1 \right\}$.
Vậy có 24 giá trị của tham số $m$ thỏa mãn bài toán đã cho.
Đáp án C.