Google
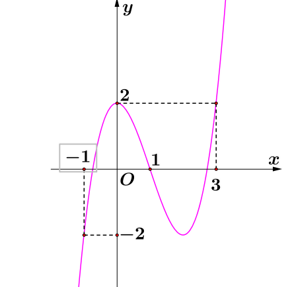
Câu hỏi: Cho hàm số $f\left( x \right)$. Đồ thị $y={f}'\left( x \right)$ cho như hình bên dưới. Hàm số $g\left( x \right)=f\left( 2-x \right)-\dfrac{1}{2}{{x}^{2}}+x$ nghịch biến trong khoảng nào dưới đây.
A. $\left( -3 ; 1 \right)$.
B. $\left( 1 ; 3 \right)$.
C. $\left( 0 ; 1 \right)$.
D. $\left( -1 ; 1 \right)$.
Ta có ${g}'\left( x \right)=-{f}'\left( 2-x \right)-x+1$.
Hàm số nghịch biến khi ${g}'\left( x \right)<0\Leftrightarrow {f}'\left( 2-x \right)>\left( 2-x \right)-1\Leftrightarrow \left[ \begin{aligned}
& -1<2-x<1 \\
& 2-x>3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 1<x<3 \\
& x<-1 \\
\end{aligned} \right.$.
Do đó hàm số $g\left( x \right)$ nghịch biến trên $\left( 1 ; 3 \right)$.
B. $\left( 1 ; 3 \right)$.
C. $\left( 0 ; 1 \right)$.
D. $\left( -1 ; 1 \right)$.
Hàm số nghịch biến khi ${g}'\left( x \right)<0\Leftrightarrow {f}'\left( 2-x \right)>\left( 2-x \right)-1\Leftrightarrow \left[ \begin{aligned}
& -1<2-x<1 \\
& 2-x>3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 1<x<3 \\
& x<-1 \\
\end{aligned} \right.$.
Do đó hàm số $g\left( x \right)$ nghịch biến trên $\left( 1 ; 3 \right)$.
Đáp án B.