Google
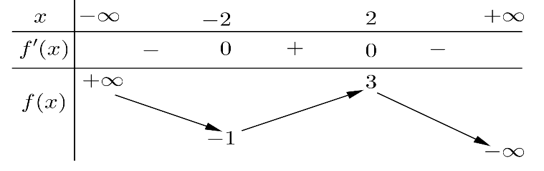
Câu hỏi: Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau
Giá trị cực tiểu của hàm số $y=f\left( x \right)+1$ bằng
A. $3$.
B. $-2$.
C. $-1$.
D. 0.
A. $3$.
B. $-2$.
C. $-1$.
D. 0.
Xét $y=f\left( x \right)+1$ :
Ta có: ${y}'={f}'\left( x \right)$ và ${y}'=0\Leftrightarrow {f}'\left( x \right)=0$ $\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right.$.
Từ bảng biến thiên, ta có: ${{y}_{CT}}=f\left( -2 \right)+1=-1+1=0$.
Ta có: ${y}'={f}'\left( x \right)$ và ${y}'=0\Leftrightarrow {f}'\left( x \right)=0$ $\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right.$.
Từ bảng biến thiên, ta có: ${{y}_{CT}}=f\left( -2 \right)+1=-1+1=0$.
Đáp án D.