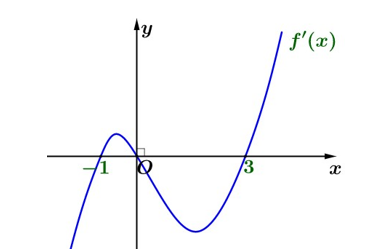
Cho hàm số đa thức $y=f\left( x \right)$ có $f\left( 0 \right)=-1$...

Đặt $u=\left| f\left( x \right)-3 \right|\to {u}'=\dfrac{\left( f\left( x \right)-3 \right).{f}'\left( x \right)}{\left| f\left( x \right)-3 \right|}$
Cho ${u}'=0\Rightarrow {f}'\left( x \right)=0\Leftrightarrow $ $\left[ \begin{aligned}
& x=-1 \\
& x=0 \\
& x=3 \\
\end{aligned} \right. $ và $ f\left( x \right)-3=0\Leftrightarrow f\left( x \right)=3\Leftrightarrow \left[ \begin{aligned}
& x=a<-1 \\
& x=b>3 \\
\end{aligned} \right.$
+ Sử dụng công thức tính diện tích hình phẳng, ta có: $f\left( 0 \right)-f\left( -1 \right)<f\left( 0 \right)-f\left( 3 \right)\Rightarrow f\left( -1 \right)>f\left( 3 \right)$.
BBT của hàm số $f\left( x \right)$
Sử dụng phương pháp ghép trục, ta có BBT của hàm số $y=f\left( \left| f\left( x \right)-3 \right| \right)=f\left( u \right)$
Vậy hàm số có 9 điểm cực trị.