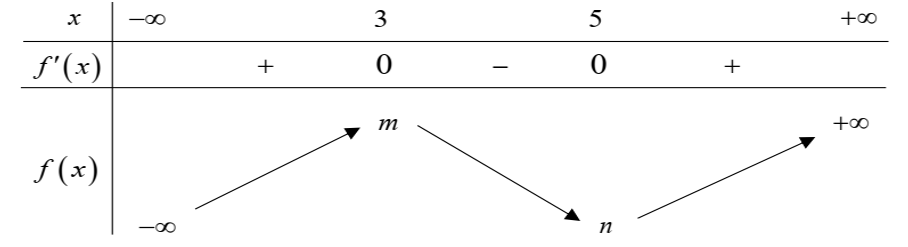
Câu hỏi: Cho hàm số bậc ba $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có bảng biến thiên như sau:
Với $m, n$ là các số nguyên thuộc đoạn $\left[ -10; 10 \right]$. Hỏi có bao nhiêu cặp số nguyên $\left( m; n \right)$ để phương trình $f\left( \left| x+5 \right| \right)=4$ có đúng 4 nghiệm phân biệt?
A. $18.$
B. $21.$
C. $19.$
D. $20.$
Với $m, n$ là các số nguyên thuộc đoạn $\left[ -10; 10 \right]$. Hỏi có bao nhiêu cặp số nguyên $\left( m; n \right)$ để phương trình $f\left( \left| x+5 \right| \right)=4$ có đúng 4 nghiệm phân biệt?
A. $18.$
B. $21.$
C. $19.$
D. $20.$
Ta có: $g\left( x \right)=f\left( \left| x+5 \right| \right)\Rightarrow {g}'\left( x \right)=\dfrac{\left( x+5 \right)}{\left| x+5 \right|}{f}'\left( \left| x+5 \right| \right)$
${g}'\left( x \right)$ không xác định tại $x=-5$
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( \left| x+5 \right| \right)=0\Leftrightarrow \left[ \begin{aligned}
& \left| x+5 \right|=3 \\
& \left| x+5 \right|=5 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-8 \\
& x=-2 \\
& x=-10 \\
& x=0 \\
\end{aligned} \right.$
Từ đó, ta có bảng biến thiên
 Từ bbt của hàm số $y=g\left( x \right)=f\left( \left| x+5 \right| \right)$, ta có
Từ bbt của hàm số $y=g\left( x \right)=f\left( \left| x+5 \right| \right)$, ta có
Phương trình $f\left( \left| x+5 \right| \right)=4$ có đúng 4 nghiệm phân biệt khi và chỉ khi đường thẳng $y=4$ cắt đồ thị hàm số $y=f\left( \left| x+5 \right| \right)$ tại đúng 4 điểm $\Leftrightarrow \left[ \begin{aligned}
& m=4 \\
& n=4 \\
\end{aligned} \right.$.
Với $m=4$ ta phải có $-10\le n<m=4$ nên có 14 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
Với $n=4$ ta phải có $4=n<m\le 10$ nên có 6 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
Vậy có 20 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
${g}'\left( x \right)$ không xác định tại $x=-5$
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( \left| x+5 \right| \right)=0\Leftrightarrow \left[ \begin{aligned}
& \left| x+5 \right|=3 \\
& \left| x+5 \right|=5 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-8 \\
& x=-2 \\
& x=-10 \\
& x=0 \\
\end{aligned} \right.$
Từ đó, ta có bảng biến thiên
Phương trình $f\left( \left| x+5 \right| \right)=4$ có đúng 4 nghiệm phân biệt khi và chỉ khi đường thẳng $y=4$ cắt đồ thị hàm số $y=f\left( \left| x+5 \right| \right)$ tại đúng 4 điểm $\Leftrightarrow \left[ \begin{aligned}
& m=4 \\
& n=4 \\
\end{aligned} \right.$.
Với $m=4$ ta phải có $-10\le n<m=4$ nên có 14 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
Với $n=4$ ta phải có $4=n<m\le 10$ nên có 6 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
Vậy có 20 cặp số nguyên $\left( m; n \right)$ thỏa ycbt.
Đáp án D.