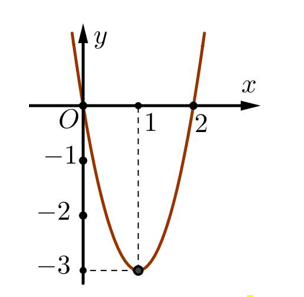
Câu hỏi: Cho $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+{{d}^{{}}}\left( a\ne 0 \right)$ là hàm số nhận giá trị không âm trên đoạn $\left[ 2;3 \right]$ có đồ thị ${f}'\left( x \right)$ như hình vẽ. Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số $g\left( x \right)=x{{f}^{2}}\left( x \right)$ ; $h\left( x \right)=-{{x}^{2}}f\left( x \right){f}'\left( x \right)$ và các đường thẳng $x=2;\ x=3$ bằng $72$. Tính $f\left( 1 \right)$.
A. $f\left( 1 \right)=2$.
B. $f\left( 1 \right)=-1$.
C. $f\left( 1 \right)=1$.
D. $f\left( 1 \right)=\dfrac{-62}{5}$.
A. $f\left( 1 \right)=2$.
B. $f\left( 1 \right)=-1$.
C. $f\left( 1 \right)=1$.
D. $f\left( 1 \right)=\dfrac{-62}{5}$.
Từ hình vẽ ta có được ${f}'\left( x \right)=3x\left( x-2 \right)=3{{x}^{2}}-6x\Rightarrow f\left( x \right)={{x}^{3}}-3{{x}^{2}}+C$.
Diện tích hình phẳng là:
$S=\int\limits_{2}^{3}{\left| g\left( x \right)-h\left( x \right) \right|\text{d}x}=\int\limits_{2}^{3}{\left| x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right) \right|\text{d}x}$
Do $x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right)\ge 0,\ \forall x\in \left[ 2;3 \right]$ nên $S=\int\limits_{2}^{3}{\left[ x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right) \right]\text{d}x}$
Ta có: $S=\int\limits_{2}^{3}{{{\left[ \dfrac{1}{2}{{x}^{2}}{{f}^{2}}\left( x \right) \right]}^{\prime }}\text{d}x}=\left. \dfrac{1}{2}{{x}^{2}}{{f}^{2}}\left( x \right) \right|_{2}^{3}=\dfrac{9}{2}{{f}^{2}}\left( 3 \right)-2{{f}^{2}}\left( 2 \right)=\dfrac{9}{2}{{C}^{2}}-2{{\left( C-4 \right)}^{2}}$
Mà $S=72\Leftrightarrow \dfrac{9}{2}{{C}^{2}}-2{{\left( C-4 \right)}^{2}}=72\Leftrightarrow \left[ \begin{matrix}
C=4 \\
C=\dfrac{-52}{5} \\
\end{matrix} \right.$.
Do $f\left( x \right)\ge 0,\ \forall x\in \left[ 2;3 \right]\Rightarrow f\left( x \right)={{x}^{3}}-3{{x}^{2}}+4\Rightarrow f\left( 1 \right)=2$.
Diện tích hình phẳng là:
$S=\int\limits_{2}^{3}{\left| g\left( x \right)-h\left( x \right) \right|\text{d}x}=\int\limits_{2}^{3}{\left| x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right) \right|\text{d}x}$
Do $x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right)\ge 0,\ \forall x\in \left[ 2;3 \right]$ nên $S=\int\limits_{2}^{3}{\left[ x{{f}^{2}}\left( x \right)+{{x}^{2}}f\left( x \right){f}'\left( x \right) \right]\text{d}x}$
Ta có: $S=\int\limits_{2}^{3}{{{\left[ \dfrac{1}{2}{{x}^{2}}{{f}^{2}}\left( x \right) \right]}^{\prime }}\text{d}x}=\left. \dfrac{1}{2}{{x}^{2}}{{f}^{2}}\left( x \right) \right|_{2}^{3}=\dfrac{9}{2}{{f}^{2}}\left( 3 \right)-2{{f}^{2}}\left( 2 \right)=\dfrac{9}{2}{{C}^{2}}-2{{\left( C-4 \right)}^{2}}$
Mà $S=72\Leftrightarrow \dfrac{9}{2}{{C}^{2}}-2{{\left( C-4 \right)}^{2}}=72\Leftrightarrow \left[ \begin{matrix}
C=4 \\
C=\dfrac{-52}{5} \\
\end{matrix} \right.$.
Do $f\left( x \right)\ge 0,\ \forall x\in \left[ 2;3 \right]\Rightarrow f\left( x \right)={{x}^{3}}-3{{x}^{2}}+4\Rightarrow f\left( 1 \right)=2$.
Đáp án A.