Cho các số thực $a,b$ thỏa mãn $a>b>0$ và ${{\log }_{2}}\left( a-b...

Ta có
$\begin{aligned}
& P={{\log }_{2}}a+{{\log }_{2}}b+2{{\log }_{2}}(a+b)-2{{\log }_{2}}({{a}^{2}}+{{b}^{2}}) \\
& \text{ =}{{\log }_{2}}ab+2{{\log }_{2}}(a-b)-2{{\log }_{2}}({{a}^{2}}+{{b}^{2}})\text{ =}{{\log }_{2}}\dfrac{ab{{(a-b)}^{2}}}{{{({{a}^{2}}+{{b}^{2}})}^{2}}} \\
\end{aligned}$
Suy ra ${{2}^{P}}=\dfrac{ab{{(a-b)}^{2}}}{{{({{a}^{2}}+{{b}^{2}})}^{2}}}$
Đặt $\dfrac{a}{b}=t(t>1)$ $\Rightarrow {{2}^{P}}=\dfrac{t{{(t-1)}^{2}}}{{{({{t}^{2}}+1)}^{2}}}=f(t)$
$\begin{aligned}
& f'(t)=\dfrac{[{{(t-1)}^{2}}+2t(t-1)]{{({{t}^{2}}+1)}^{2}}t{{(t-1)}^{2}}.2.({{t}^{2}}+1).2t}{{{({{t}^{2}}+1)}^{4}}}\text{ =}\dfrac{(3{{t}^{2}}-4t+1)({{t}^{2}}+1)4{{t}^{2}}{{(t-1)}^{2}}}{{{({{t}^{2}}+1)}^{3}}} \\
& \text{ =}\dfrac{-{{t}^{4}}+4{{t}^{3}}4t+1}{{{({{t}^{2}}+1)}^{3}}} \\
\end{aligned}$
$\begin{aligned}
& f'(t)=0\Leftrightarrow -{{t}^{4}}+4{{t}^{3}}4t+1=0\Leftrightarrow \left[ \begin{aligned}
& t=\pm 1 \\
& t=2\pm \sqrt{3} \\
\end{aligned} \right. \\
& \\
\end{aligned}$

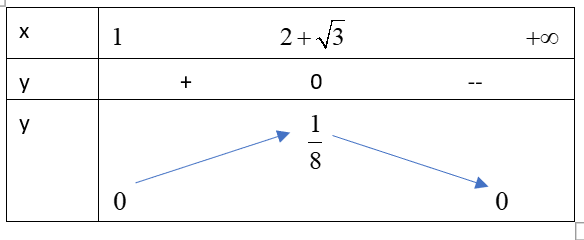
Hàm số đạt max khi $t=\dfrac{a}{b}=2+\sqrt{3}\Rightarrow a=\left( 2+\sqrt{3} \right)b$
Suy ra $\text{ }{{\log }_{2}}\left[ \left( 2+\sqrt{3} \right)b-b \right]={{\log }_{2}}\left[ \left( 2+\sqrt{3} \right)b+b \right]$
$\Leftrightarrow {{\log }_{2}}\left( 1+\sqrt{3} \right)b={{\log }_{2}}\left( 3+\sqrt{3} \right)b$
$\Rightarrow b\approx 0.936\Rightarrow a-b=\left( 1+\sqrt{3} \right)b\approx 2.558\in \left( 2;3 \right)$.