Câu hỏi: Chứng minh công thức \(\tan \dfrac{\alpha }{2} = \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}\) (với \(0 < \alpha < \dfrac{\pi }{2}\)) bằng “phương pháp hình học “ như sau:
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2},\widehat B = \alpha \). Bằng cách vẽ đường phân giác BD của góc B (h. 6.5), từ tính chất \(\dfrac{{AD}}{{AB}} = \dfrac{{DC}}{{BC}}\), hãy suy ra rằng:
\(\tan \dfrac{\alpha }{2} = \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}.\) Hãy tính \(\tan \dfrac{\pi }{{12}}\).
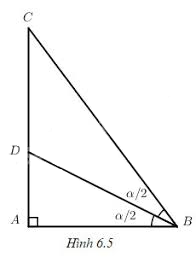
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2},\widehat B = \alpha \). Bằng cách vẽ đường phân giác BD của góc B (h. 6.5), từ tính chất \(\dfrac{{AD}}{{AB}} = \dfrac{{DC}}{{BC}}\), hãy suy ra rằng:
\(\tan \dfrac{\alpha }{2} = \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}.\) Hãy tính \(\tan \dfrac{\pi }{{12}}\).

Lời giải chi tiết
Ta có
\(\begin{array}{l}\dfrac{{AD}}{{AB}} = \dfrac{{DC}}{{BC}} = \dfrac{{AC - AD}}{{BC}}\\ = \dfrac{{AC}}{{BC}} - \dfrac{{AD}}{{AB}}.\dfrac{{AB}}{{BC}}\end{array}\)
Từ đó \(\dfrac{{AD}}{{AB}}\left( {1 + \dfrac{{AB}}{{BC}}} \right) = \dfrac{{AC}}{{BC}},\) tức là \(\tan \dfrac{\alpha }{2}\left( {1 + \cos \alpha } \right) = \sin \alpha \), suy ra \(\tan \dfrac{\alpha }{2} = \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}\).
Với \(\alpha = \dfrac{\pi }{6}\) ta được \(\tan \dfrac{\pi }{{12}} = \dfrac{1}{{2\left( {1 + \dfrac{{\sqrt 3 }}{2}} \right)}} = \dfrac{1}{{2 + \sqrt 3 }} = 2 - \sqrt 3 .\)
Ta có
\(\begin{array}{l}\dfrac{{AD}}{{AB}} = \dfrac{{DC}}{{BC}} = \dfrac{{AC - AD}}{{BC}}\\ = \dfrac{{AC}}{{BC}} - \dfrac{{AD}}{{AB}}.\dfrac{{AB}}{{BC}}\end{array}\)
Từ đó \(\dfrac{{AD}}{{AB}}\left( {1 + \dfrac{{AB}}{{BC}}} \right) = \dfrac{{AC}}{{BC}},\) tức là \(\tan \dfrac{\alpha }{2}\left( {1 + \cos \alpha } \right) = \sin \alpha \), suy ra \(\tan \dfrac{\alpha }{2} = \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}\).
Với \(\alpha = \dfrac{\pi }{6}\) ta được \(\tan \dfrac{\pi }{{12}} = \dfrac{1}{{2\left( {1 + \dfrac{{\sqrt 3 }}{2}} \right)}} = \dfrac{1}{{2 + \sqrt 3 }} = 2 - \sqrt 3 .\)