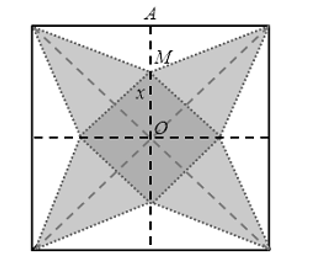
Câu hỏi: Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết các cạnh hình vuông bằng $20 cm$, $OM=x \left( cm \right)$. Tìm $x$ để hình chóp đều ấy có thể tích lớn nhất
A. $x=9 cm$.
B. $x=8 cm$.
C. $x=6 cm$.
D. $x=7 cm$.

Giả sử được hình chóp tứ giác đều như hình vẽ
Ta có: Cạnh đáy bằng $x\sqrt{2}$.
+ $OM=x$ $\Rightarrow OH=HM=\dfrac{x}{\sqrt{2}}$ $\Rightarrow SH=10\sqrt{2}-\dfrac{x}{\sqrt{2}}$.
+ $SO=\sqrt{S{{H}^{2}}-O{{H}^{2}}}=\sqrt{{{\left( 10\sqrt{2}-\dfrac{x}{\sqrt{2}} \right)}^{2}}-{{\left( \dfrac{x}{\sqrt{2}} \right)}^{2}}}=\sqrt{20\left( 10-x \right)}$.
Thể tích $V=\dfrac{1}{3}.{{S}_{MNPQ}}.SO$ $=\dfrac{1}{3}.2{{x}^{2}}.\sqrt{20\left( 10-x \right)}$ $=\dfrac{\sqrt{20}}{3}.{{x}^{2}}.\sqrt{40-4x}$, (với $0\le x\le 10$ ).
Tìm GTLN của $V$ ta được ${{V}_{\max }}=\dfrac{\sqrt{20}}{3}{{.10}^{2}}$ khi $x=8$.
* Cách 2
Áp dụng BĐT Cauchy cho 4 số không âm, ta có:
${{x}^{2}}.\sqrt{40-4x}=\sqrt{\left( 40-4x \right).x.x.x.x}.\le {{\left( \sqrt{\dfrac{40-4x+x+x+x+x}{4}} \right)}^{4}}$ $\Leftrightarrow \sqrt{40-4x}.{{x}^{2}}\le {{10}^{2}}$.
Vậy $V=\dfrac{\sqrt{20}}{3}.{{x}^{2}}\sqrt{40-4x}\le \dfrac{\sqrt{20}}{3}{{.10}^{2}}$. Dấu bằng xảy ra khi $40-4x=x\Leftrightarrow x=8$.
A. $x=9 cm$.
B. $x=8 cm$.
C. $x=6 cm$.
D. $x=7 cm$.
Giả sử được hình chóp tứ giác đều như hình vẽ
Ta có: Cạnh đáy bằng $x\sqrt{2}$.
+ $OM=x$ $\Rightarrow OH=HM=\dfrac{x}{\sqrt{2}}$ $\Rightarrow SH=10\sqrt{2}-\dfrac{x}{\sqrt{2}}$.
+ $SO=\sqrt{S{{H}^{2}}-O{{H}^{2}}}=\sqrt{{{\left( 10\sqrt{2}-\dfrac{x}{\sqrt{2}} \right)}^{2}}-{{\left( \dfrac{x}{\sqrt{2}} \right)}^{2}}}=\sqrt{20\left( 10-x \right)}$.
Thể tích $V=\dfrac{1}{3}.{{S}_{MNPQ}}.SO$ $=\dfrac{1}{3}.2{{x}^{2}}.\sqrt{20\left( 10-x \right)}$ $=\dfrac{\sqrt{20}}{3}.{{x}^{2}}.\sqrt{40-4x}$, (với $0\le x\le 10$ ).
Tìm GTLN của $V$ ta được ${{V}_{\max }}=\dfrac{\sqrt{20}}{3}{{.10}^{2}}$ khi $x=8$.
* Cách 2
Áp dụng BĐT Cauchy cho 4 số không âm, ta có:
${{x}^{2}}.\sqrt{40-4x}=\sqrt{\left( 40-4x \right).x.x.x.x}.\le {{\left( \sqrt{\dfrac{40-4x+x+x+x+x}{4}} \right)}^{4}}$ $\Leftrightarrow \sqrt{40-4x}.{{x}^{2}}\le {{10}^{2}}$.
Vậy $V=\dfrac{\sqrt{20}}{3}.{{x}^{2}}\sqrt{40-4x}\le \dfrac{\sqrt{20}}{3}{{.10}^{2}}$. Dấu bằng xảy ra khi $40-4x=x\Leftrightarrow x=8$.
Đáp án B.