Câu hỏi: Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c.
a) Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau;
b) Tính VABCD theo a, b, c;
c) Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
a) Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau;
b) Tính VABCD theo a, b, c;
c) Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
Lời giải chi tiết
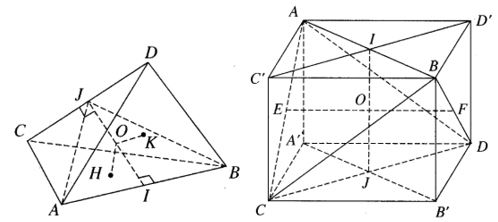
A) Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'. A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.
b) Đặt AC' = x, AD' = y, AA' = z.
Ta có:
\(\left\{ \begin{array}{l}{x^2} + {y^2} = {c^2}\\{x^2} + {z^2} = {b^2}\\{y^2} + {z^2} = {a^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = \frac{{{c^2} + {b^2} - {a^2}}}{2}\\{y^2} = \frac{{{a^2} + {c^2} - {b^2}}}{2}\\{z^2} = \frac{{{b^2} + {a^2} - {c^2}}}{2}\end{array} \right.\)
Từ đó suy ra VABCD = VAC'BD'. A'CB'D/3\(= \frac{1}{{12}}.\sqrt {2\left( {{a^2} + {b^2} - {c^2}} \right)\left({{a^2} + {c^2} - {b^2}} \right)\left({{b^2} + {c^2} - {a^2}} \right)} \)
c) Ta có O là tâm của hình hộp chữ nhật AC'BD'. A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
\(r = \frac{{AB'}}{2} = \frac{{\sqrt {{x^2} + {y^2} + {z^2}} }}{2}\) \(= \frac{{\sqrt {2\left( {{a^2} + {b^2} + {c^2}} \right)} }}{8}\)
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có VABCD = VOABC + VOBCD + VOCDA + VODAB
= 4VOABC = 4r'SABC/3
Do đó:
\(r' = \frac{3}{4}.\frac{{{V_{ABCD}}}}{{{S_{ABC}}}}\) \(= \frac{1}{{16}}.\frac{{\sqrt {2\left( {{a^2} + {b^2} - {c^2}} \right)\left({{a^2} + {c^2} - {b^2}} \right)\left({{b^2} + {c^2} - {a^2}} \right)} }}{{\sqrt {p\left({p - a} \right)\left({p - b} \right)\left({p - c} \right)} }}\)
Trong đó \(p = \frac{{a + b + c}}{2}\).
A) Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'. A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.
b) Đặt AC' = x, AD' = y, AA' = z.
Ta có:
\(\left\{ \begin{array}{l}{x^2} + {y^2} = {c^2}\\{x^2} + {z^2} = {b^2}\\{y^2} + {z^2} = {a^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = \frac{{{c^2} + {b^2} - {a^2}}}{2}\\{y^2} = \frac{{{a^2} + {c^2} - {b^2}}}{2}\\{z^2} = \frac{{{b^2} + {a^2} - {c^2}}}{2}\end{array} \right.\)
Từ đó suy ra VABCD = VAC'BD'. A'CB'D/3\(= \frac{1}{{12}}.\sqrt {2\left( {{a^2} + {b^2} - {c^2}} \right)\left({{a^2} + {c^2} - {b^2}} \right)\left({{b^2} + {c^2} - {a^2}} \right)} \)
c) Ta có O là tâm của hình hộp chữ nhật AC'BD'. A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
\(r = \frac{{AB'}}{2} = \frac{{\sqrt {{x^2} + {y^2} + {z^2}} }}{2}\) \(= \frac{{\sqrt {2\left( {{a^2} + {b^2} + {c^2}} \right)} }}{8}\)
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có VABCD = VOABC + VOBCD + VOCDA + VODAB
= 4VOABC = 4r'SABC/3
Do đó:
\(r' = \frac{3}{4}.\frac{{{V_{ABCD}}}}{{{S_{ABC}}}}\) \(= \frac{1}{{16}}.\frac{{\sqrt {2\left( {{a^2} + {b^2} - {c^2}} \right)\left({{a^2} + {c^2} - {b^2}} \right)\left({{b^2} + {c^2} - {a^2}} \right)} }}{{\sqrt {p\left({p - a} \right)\left({p - b} \right)\left({p - c} \right)} }}\)
Trong đó \(p = \frac{{a + b + c}}{2}\).