Câu hỏi: Cho lăng trụ ABC. A'B'C'
a) Tính tỉ số \(\frac{{{V_{ACA'B'}}}}{{{V_{ABC. A'B'C'}}}}\)
b) Tính VACA'B' biết rằng tam giác ABC là tam giác đều cạnh bằng a, AA' = b và AA' tạo với (ABC) một góc bằng 60o
a) Tính tỉ số \(\frac{{{V_{ACA'B'}}}}{{{V_{ABC. A'B'C'}}}}\)
b) Tính VACA'B' biết rằng tam giác ABC là tam giác đều cạnh bằng a, AA' = b và AA' tạo với (ABC) một góc bằng 60o
Lời giải chi tiết
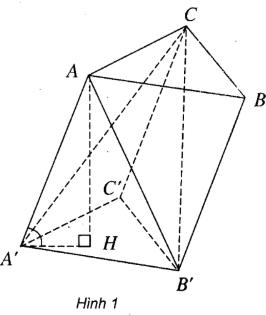
A) Ta có: VACA'B' = VB'. ACA' = VB'. CA'C' = VC. A'B'C' = VABC. A'B'C'/3
Từ đó suy ra tỉ số phải tìm bằng 1/3.
b) Gọi H là chân đường cao đi qua A của lăng trụ.
\(\Rightarrow \left( {AA',\left( {A'B'C'} \right)} \right) = \left({AA', A'H} \right)\) \(= \widehat {AA'H} = {60^0}\)
Tam giác vuông AA’H có \(AH = AA'\sin {60^0} = \frac{{b\sqrt 3 }}{2}\)
Lại có \({S_{A'B'C'}} = \frac{1}{2}A'B'. A'C'.\sin \widehat {B'A'C'}\) \(= \frac{1}{2}. A. A.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
Do đó: \({V_{ABC. A'B'C'}} = {S_{A'B'C'}}. AH\) \(= \frac{{{a^2}\sqrt 3 }}{4}.\frac{{b\sqrt 3 }}{2} = \frac{{3{a^2}b}}{8}\)
Suy ra \({V_{ACA'B'}} = \frac{1}{3}{V_{ABC. A'B'C'}} \) \(= \frac{1}{3}.\frac{{3{a^2}b}}{8} = \frac{{{a^2}b}}{8}\)
A) Ta có: VACA'B' = VB'. ACA' = VB'. CA'C' = VC. A'B'C' = VABC. A'B'C'/3
Từ đó suy ra tỉ số phải tìm bằng 1/3.
b) Gọi H là chân đường cao đi qua A của lăng trụ.
\(\Rightarrow \left( {AA',\left( {A'B'C'} \right)} \right) = \left({AA', A'H} \right)\) \(= \widehat {AA'H} = {60^0}\)
Tam giác vuông AA’H có \(AH = AA'\sin {60^0} = \frac{{b\sqrt 3 }}{2}\)
Lại có \({S_{A'B'C'}} = \frac{1}{2}A'B'. A'C'.\sin \widehat {B'A'C'}\) \(= \frac{1}{2}. A. A.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
Do đó: \({V_{ABC. A'B'C'}} = {S_{A'B'C'}}. AH\) \(= \frac{{{a^2}\sqrt 3 }}{4}.\frac{{b\sqrt 3 }}{2} = \frac{{3{a^2}b}}{8}\)
Suy ra \({V_{ACA'B'}} = \frac{1}{3}{V_{ABC. A'B'C'}} \) \(= \frac{1}{3}.\frac{{3{a^2}b}}{8} = \frac{{{a^2}b}}{8}\)