Câu hỏi: Cho tứ diện \(ABCD\). Gọi \(G_1\), \(G_2\), \(G_3\) lần lượt là trọng tâm các tam giác \(ABC\), \(ACD\), \(ABD\). Chứng minh rằng \((G_1G_2G_3)\parallel(BCD)\).
Phương pháp giải
Sử dụng tính chất của trọng tâm trong tam giác.
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với \(d’\) nằm trong \((\alpha)\) thì \(d\) song song với \((\alpha)\).
\(\left\{ \begin{array}{l}d \not\subset (\alpha)\\d\parallel d'\\d' \subset (\alpha)\end{array} \right. \Rightarrow d\parallel (\alpha)\)
Sử dụng tính chất: Nếu mặt phẳng \((\alpha)\) chứa hai đường thẳng cắt nhau \(a, b\) và hai đường thẳng này cùng song song với mặt phẳng \((\beta)\) thì mặt phẳng \((\alpha)\) song song với mặt phẳng \((\beta)\).
\(\left\{ \begin{array}{l}a \subset (\alpha), b \subset (\alpha)\\a \text{ cắt } b\\a\parallel (\beta), b\parallel (\beta)\end{array} \right. \Rightarrow (\alpha)\parallel (\beta)\)
Lời giải chi tiết
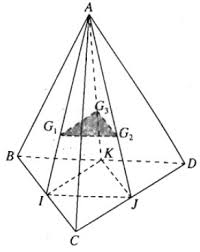
Gọi \(I, J, K\) lần lượt là trung điểm của \(BC, CD, BD\).
Theo tính chất trọng tâm của tam giác ta có:
\(\dfrac{AG_1}{AI}=\dfrac{AG_2}{AJ}=\dfrac{AG_3}{AK}=\dfrac{2}{3}\).
Theo định lý Ta let suy ra: \(G_1G_2\parallel IJ\) mà \(IJ\subset (BCD)\)
\(\Rightarrow G_1G_2\parallel(BCD)\).
Tương tự ta có \(G_2G_3\parallel (BCD)\).
Ta lại có \(G_1G_2, G_2G_3\subset (G_1G_2G_3)\)
\(\Rightarrow (G_1G_2G_3)\parallel (BCD)\).
Sử dụng tính chất của trọng tâm trong tam giác.
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với \(d’\) nằm trong \((\alpha)\) thì \(d\) song song với \((\alpha)\).
\(\left\{ \begin{array}{l}d \not\subset (\alpha)\\d\parallel d'\\d' \subset (\alpha)\end{array} \right. \Rightarrow d\parallel (\alpha)\)
Sử dụng tính chất: Nếu mặt phẳng \((\alpha)\) chứa hai đường thẳng cắt nhau \(a, b\) và hai đường thẳng này cùng song song với mặt phẳng \((\beta)\) thì mặt phẳng \((\alpha)\) song song với mặt phẳng \((\beta)\).
\(\left\{ \begin{array}{l}a \subset (\alpha), b \subset (\alpha)\\a \text{ cắt } b\\a\parallel (\beta), b\parallel (\beta)\end{array} \right. \Rightarrow (\alpha)\parallel (\beta)\)
Lời giải chi tiết
Gọi \(I, J, K\) lần lượt là trung điểm của \(BC, CD, BD\).
Theo tính chất trọng tâm của tam giác ta có:
\(\dfrac{AG_1}{AI}=\dfrac{AG_2}{AJ}=\dfrac{AG_3}{AK}=\dfrac{2}{3}\).
Theo định lý Ta let suy ra: \(G_1G_2\parallel IJ\) mà \(IJ\subset (BCD)\)
\(\Rightarrow G_1G_2\parallel(BCD)\).
Tương tự ta có \(G_2G_3\parallel (BCD)\).
Ta lại có \(G_1G_2, G_2G_3\subset (G_1G_2G_3)\)
\(\Rightarrow (G_1G_2G_3)\parallel (BCD)\).