Câu hỏi: Xét khối nón
A.
B.
C.
D.
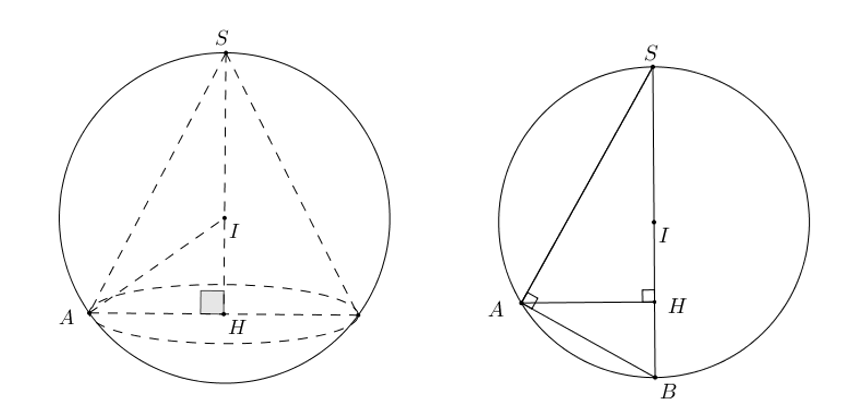 Gọi
Gọi
TH1:
Ta có
Suy ra
Suy ra
TH2:
Ta có
Suy ra
A.
B.
C.
D.
TH1:
Ta có
Suy ra
Suy ra
TH2:
Ta có
Suy ra
Đáp án B.